Что такое лямбда размерность от чего зависит физический смысл

Обновлено: 07.07.2024

Уравнение теплопроводности имеет вид

где — оператор Лапласа по . Это уравнение является примером уравнения параболического типа. Этому уравнению подчиняется температура однородной и изотропной среды (в этом случае — температура среды в точке в момент времени t). Точно также этому уравнению удовлетворяет плотность диффундирующего вещества, например, плотность броуновских частиц в случае, когда частиц достаточно много, так что мы можем говорить об их плотности и об изменении этой плотности как о непрерывном процессе. Поэтому уравнение (6.1) часто называют также уравнением диффузии.

Вывод уравнения теплопроводности для температуры основан на следующих естественных физических гипотезах:

1. Количество тепла Q, необходимое для нагрева куска рассматриваемого вещества массы m от температуры до температуры пропорционально m и

(коэффициент с называется удельной теплоемкостью).

2. Количество тепла передающееся через площадку площади время пропорционально и скорости роста температуры и по направлению нормали п к этой площадке (закон Фурье):

где коэффициент называется коэффициентом теплопроводности и, как и удельная теплоёмкость, характеризует свойства среды; знак минус означает, что тепло передаётся по направлению, противоположному направлению роста температуры.

Следует иметь в виду, что обе гипотезы являются лишь приближениями, как и вытекающее из них уравнение (6.1).

Как мы увидим ниже, из уравнения (6.1) следует, например, что скорость распространения тепла бесконечна, что физически абсурдно. Однако в большинстве технических задач сделанные предположения и уравнение (6.1) в достаточной степени оправданы. Более точная модель теплопередачи должна была бы учитывать молекулярную структуру вещества, что приводит к задачам статистической физики, неизмеримо более сложным, чем решение модельного уравнения (6.1).

Отметим, впрочем, что независимо от физического смысла уравнение (6.1) и аналогичные уравнения играют важную роль в математике. Они используются, например, для изучения эллиптических уравнений.

Приведём вывод уравнения теплопроводности (при ). Используем закон сохранения энергии (в данном случае тепла) в некотором объёме . Будем считать, что П имеет гладкую границу . Скорость изменения тепловой энергии вещества в объёме П равна, очевидно,

где р — объёмная плотность вещества, — элемент объёма в . Считая , мы получим

Пусть теперь Р — скорость истечения тепла через границу . Ясно, что

где внешняя нормаль к — элемент площади . В правой части здесь написан поток вектора через границу . По формуле Гаусса-Остроградского имеем:

Закон сохранения тепловой энергии при отсутствии источников тепла означает, что

Почему мыльные пузыри круглые, а водомерки не тонут? Все это следствия одного и того же физического явления, без которого вода не была бы водой.

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие и характеристики поверхностного натяжения

С явлением поверхностного натяжения жидкости мы сталкиваемся каждый день:

капли воды стремятся принять форму, близкую к шарообразной (а в невесомости они совсем шарообразные);
струя воды из-под крана стремится к цилиндрической форме;
булавка не тонет на поверхности воды в стакане;
многие насекомые могут скользить по поверхности воды.

Силы поверхностного натяжения действуют вдоль поверхности жидкости, стремясь сократить ее площадь. Как будто жидкость заключена в упругую пленку, которая стремится сжать свое содержимое.

Потенциальная энергия взаимного притяжения молекул жидкости больше их кинетической энергии. Это позволяет веществу сохранять объем (но не форму), и этот объем ограничивается поверхностью жидкости.

На молекулу жидкости, которая находится внутри, действуют силы притяжения со стороны других молекул, и они уравновешивают друг друга. А на ту молекулу, что находится на поверхности, действуют силы притяжения не только со стороны других молекул жидкости, но и со стороны газа (внешней среды). Эти вторые значительно меньше первых, поэтому равнодействующая сила притяжения направлена внутрь жидкости, что способствует удержанию молекулы на поверхности.

Поверхностное натяжение — это стремление жидкости сократить свою свободную поверхность, то есть уменьшить избыток своей потенциальной энергии на границе раздела с газообразной фазой.

Чем больше площадь поверхности жидкости, тем больше молекул, которые обладают избыточной потенциальной энергией, и тем больше поверхностная энергия. Этот факт можно записать в виде следующего соотношения:

Поверхностная энергия жидкости

W = σS

W — поверхностная энергия жидкости [Дж]

S — площадь свободной поверхности [м 2 ]

σ — коэффициент поверхностного натяжения [Н/м]

Отсюда мы можем вывести формулу коэффициента поверхностного натяжения.

Коэффициент поверхностного натяжения — это физическая величина, которая характеризует данную жидкость и численно равна отношению поверхностной энергии к площади свободной поверхности жидкости.

Коэффициент поверхностного натяжения

σ = W/S

W — поверхностная энергия жидкости [Дж]

S — площадь свободной поверхности [м 2 ]

σ — коэффициент поверхностного натяжения [Н/м]

Коэффициент поверхностного натяжения жидкости зависит:

от природы жидкости;
температуры жидкости;
свойств газа, который граничит с данной жидкостью;
наличия поверхностно-активных веществ (например, мыло или стиральный порошок), которые уменьшают поверхностное натяжение.

Коэффициент поверхностного натяжения не зависит от площади свободной поверхности жидкости, хотя может быть рассчитан с ее помощью.

Если на жидкость не действуют другие силы или их действие мало, жидкость будет стремиться принимать форму сферы, как капля воды или мыльный пузырь. Так же ведет себя вода в невесомости. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, стягивающие эту поверхность. Эти силы называются силами поверхностного натяжения.

Сила поверхностного натяжения

F = σl

F — сила поверхностного натяжения [Н]

l — длина контура, ограничивающего поверхность жидкости [м]

σ — коэффициент поверхностного натяжения [Н/м]

В химической промышленности в воду часто добавляют специальные реагенты-смачиватели, не дающие ей собираться в капли на какой-либо поверхности. Например, их добавляют в жидкие средства для посудомоечных машин. Попадая в поверхностный слой воды, молекулы таких реагентов заметно ослабляют силы поверхностного натяжения, вода не собирается в капли и не оставляет на поверхности пятен после высыхания.

Поверхностное натяжение некоторых жидкостей на границе с воздухом

Поверхностное натяжение, 10 −3 Н/м

Хлорид натрия (водный раствор)

Азотная кислота 70%

Серная кислота 85%

Пример решения задачи

Тонкое алюминиевое кольцо радиусом 7,8 см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Температуру раствора считать комнатной. Масса кольца 7 г. Коэффициент поверхностного натяжения мыльного раствора при комнатной температуре равен 4 × 10 -2 Н/м.

Решение

На кольцо действуют сила тяжести, сила поверхностного натяжения и внешняя сила, с которой отрывают кольцо от раствора.

Так как кольцо соприкасается с раствором и внешней и внутренней сторонами, то сила поверхностного натяжения удваивается:

Контур, ограничивающий поверхность жидкости, имеет форму окружности. Значит, его длина будет равна:

Подставляем в формулу силы поверхностного натяжения:

Условие отрыва кольца от поверхности раствора имеет вид второго закона Ньютона для инерциальных систем отсчета:

Подставляем силу поверхностного натяжения:

F = 0,007 × 10 + 4 × 4 × 10 -2 × 3,14 × 7,8 × 10 -2 = 0,11 Н

Ответ: Для того, чтобы оторвать кольцо от раствора, необходимо приложить силу в 0,11 Н.

Важность поверхностного натяжения

Выше мы уже показали, что поверхностное натяжение встречается в повседневной жизни достаточно часто. Но на самом деле оно встречается еще чаще!

В некоторых отраслях промышленности поверхностное натяжение используют как простой показатель загрязнения продуктов. Поскольку оно определяется на молекулярном уровне, любое изменение компонентов вещества может привести к изменению этого показателя. То есть если мы знаем, каким должно быть поверхностное натяжение совершенно чистого вещества, то по отклонению от этой нормы мы можем установить уровень его загрязнения.

Не только человек, но и представители живой природы используют физические явления в своих целях. Например, за счет поверхностного натяжения насекомые водомерки могут перемещаться по водной глади, не промочив лапки. Конечности водомерки отталкивают воду и захватывают воздух, что позволяет насекомым продавливать поверхность воды, не нарушая ее.

За счет поверхностного натяжения возникает такое любопытное явление, как ламинарное течение. Это упорядоченный режим течения вязкой жидкости или газа, при котором соседние слои жидкости не перемешиваются. Выглядит ламинарная струя так, как будто вода застыла.

И это еще не все: поверхностное натяжение позволяет предметам плавать, благодаря ему выживают и развиваются экосистемы, и даже состав воды стабилен только за счет этого явления. Без него вода бы постоянно находилась на границе двух агрегатных состояний: испарялась и вновь конденсировалась, так как молекулы легко выскакивали бы с ее поверхности.

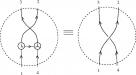
Лямбда-исчисление — это формальная система в математической логике для выражения подсчетов на основе абстракции и применения функций с использованием привязки и подстановки переменных. Это универсальная модель, которую можно применять для проектирования любой машины Тьюринга. Впервые введена лямбда-исчисления Черчем, известным математиком, в 1930-х годах.

Система состоит из построения лямбда-членов и выполнения над ними операций сокращения.

Пояснения и приложения

Греческая буква lambda (λ) используется в лямбда-выражениях и лямбда-терминах для обозначения связывания переменной в функции.

Лямбда-исчисление может быть нетипизировано или типизировано. В первом варианте функции могут быть применены только в том случае, если они способны принимать данные этого типа. Типизированные лямбда-исчисления слабее, могут выражать меньшее значение. Но, с другой стороны, они позволяют доказывать больше вещей.

Одной из причин того, что существует много разных типов — это желание ученых сделать больше, не отказываясь от возможности доказывать сильные теоремы лямбда-исчислений.

Система находит применение во многих различных областях математики, философии, лингвистики, и компьютерных наук. В первую очередь, лямбда-исчисления — это расчет, который сыграл важную роль в развитии теории языков программирования. Именно стили функционального создания реализуют системы. Они также являются актуальной темой исследований в теории этих категорий.

Для чайников

Лямбда-исчисление была введена математиком Алонзо Черчем в 1930-х годах в рамках исследования основ науки. Первоначальная система была показана как логически несовместимая в 1935 году, когда Стивен Клин и Дж. Б. Россер разработали парадокс Клини-Россера.

В последствии, в 1936 году Черч выделил и опубликовал только ту часть, которая имеет отношение к расчетам, то, что сейчас называется нетипизированным лямбда-исчислением. В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.

До 1960-х годов, когда выяснилось его отношение к языкам программирования, λ стала лишь формализмом. Благодаря применениям Ричарда Монтегю и других лингвистов в семантике естественного языка, исчисление стало занимать почетное место как в лингвистике, так и в информатике.

Происхождение символа

Введение в лямбда исчисление

Система состоит из языка терминов, которые выбираются определенным формальным синтаксисом, и набора правил преобразования, которые позволяют манипулировать ими. Последний пункт можно рассматривать как эквациональную теорию или как операционное определение.

Все функции в лямбда-исчислении являются анонимными, то есть не имеющими имен. Они принимают только одну входную переменную, при этом каррирование используется для реализации графиков с несколькими непостоянными.

Лямбда-термины

Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически допустимых понятий:

Переменная x сама по себе является действительным лямбда-термином:

если T это ЛТ, и x непостоянная, то (lambda xt) называется абстракцией.
если T, а также s понятия, то (TS) называется приложением.

Ничто другое не является лямбда-термином. Таким образом, понятие действительно тогда и только тогда, когда оно может быть получено повторным применением этих трех правил. Тем не менее некоторые скобки могут быть опущены в соответствии с другими критериями.

Определение

Лямбда-выражения состоят из:

переменных v 1, v 2. v n.
символов абстракции 'λ' и точки '.'
скобок ().

Множество Λ, может быть определено индуктивно:

Если x переменная, то x ∈ Λ;
x непостоянная и M ∈ Λ, то (λx.M) ∈ Λ;
M, N ∈ Λ, то (MN) ∈ Λ.

Обозначение

Чтобы сохранить нотацию лямбда-выражений в незагроможденном виде, обычно применяются следующие соглашения:

Внешние скобки опущены: MN вместо (MN).
Предполагается, что приложения остаются ассоциативными: взамен ((MN) P) можно написать MNP.
Тело абстракции простирается дальше вправо: λx.MN означает λx. (MN), а не (λx.M) N.
Сокращается последовательность абстракций: λx.λy.λz.N можно λxyz.N.

Свободные и связанные переменные

Оператор λ соединяет свою непостоянную, где бы он ни находился в теле абстракции. Переменные, попадающие в область, называются связанными. В выражении λ x. М, часть λ х часто называют связующим. Как бы намекая, что переменные становятся группой с добавлением Х х к М. Все остальные неустойчивые называются свободными.

Множество свободных переменных M обозначается как FV (M) и определяется рекурсией по структуре терминов следующим образом:

FV (x) = , где x - переменная.
FV (λx.M) = FV (M) \ .
FV (MN) = FV (M) ∪ FV (N).

Формула, которая не содержит свободных переменных, называется закрытой. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны терминам в комбинаторной логике.

Сокращение

Значение лямбда-выражений определяется тем, как они могут быть сокращены.

Существует три вида урезания:

α-преобразование: изменение связанных переменных (альфа).
β-редукция: применение функций к своим аргументам (бета).
η-преобразование: охватывает понятие экстенсиональности.

Здесь речь также идет о полученных эквивалентностях: два выражения являются β-эквивалентными, если они могут быть β-преобразованы в одно и то же составляющее, а α / η-эквивалентность определяется аналогично.

Термин redex, сокращение от приводимого оборота, относится к подтемам, которые могут быть сокращены одним из правил. Лямбда исчисление для чайников, примеры:

(λ x.M) N является бета-редексом в выражении замены N на x в M. Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].

Если x не является свободной в M, λ х. М х также ет-REDEX с регулятором М.

α-преобразование

Альфа-переименования позволяют изменять имена связанных переменных. Например, λ x. х может дать λ у. у. Термины, которые отличаются только альфа-преобразованием, называются α-эквивалентными. Часто при использовании лямбда-исчисления α-эквивалентные считаются взаимными.

Точные правила для альфа-преобразования не совсем тривиальны. Во-первых, при данной абстракции переименовываются только те переменные, которые связаны с одной и той же системой. Например, альфа-преобразование λ x.λ x. x может привести к λ y.λ x. х, но это может не ввергнуть к λy.λx.y Последний имеет иной смысл, чем оригинал. Это аналогично понятию программирования затенения переменных.

Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату непостоянной другой абстракцией. Например, если заменить x на y в λ x.λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.

В языках программирования со статической областью видимости альфа-преобразование можно использовать для упрощения разрешения имен. При этом следя за тем, чтобы понятие переменной не маскировало обозначение в содержащей области.

В нотации индекса Де Брюйна любые два альфа-эквивалентных термина синтаксически идентичны.

Замена

Изменения, написанные Е [V: = R], представляют собой процесс замещения всех свободных вхождений переменной V в выражении Е с оборотом R. Подстановка в терминах λ определяется лямбдой исчисления рекурсии по структуре понятий следующим образом (примечание: x и y - только переменные, а M и N - любое λ-выражение).

y [x: = N] ≡ y, если x ≠ y

(M 1 M 2) [x: = N] ≡ (M 1 [x: = N]) (M 2 [x: = N])

(λ x.M) [x: = N] ≡ λ x.M

(λ y.M) [x: = N] y λ y. (M [x: = N]), если x ≠ y, при условии, что y ∉ FV (N).

Для подстановки в лямбда-абстракцию иногда необходимо α-преобразовать выражение. Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.

β-редукция

Бета-редукция отражает идею применения функции. Бета-восстановительный определяется в терминах замещения: ((X V. E) Е ') является Е [V: = Е'].

Например, предполагая некоторое кодирование 2, 7, ×, имеется следующее β-уменьшение: ((λ n. N × 2) 7) → 7 × 2.

Бета-редукция может рассматриваться как то же самое, что и концепция локальной сводимости при естественной дедукции через изоморфизм Карри – Ховарда.

η-преобразование

Эта-конверсия выражает идею экстенсиональности, которая в этом контексте заключается в том, что две функции равны тогда, когда они дают одинаковый результат для всех аргументов. Эта конвертация обменивает между λ x. (F x) и f всякий раз, когда x не кажется свободным в f.

Данное действие может рассматриваться как то же самое, что и концепция локальной полноты в естественной дедукции через изоморфизм Карри – Ховарда.

Нормальные формы и слияние

Для нетипизированного лямбда-исчисления β-редукция как правило переписывания не является ни сильно нормализующей, ни слабо.

Тем не менее можно показать, что β-редукция сливается при работе до α-преобразования (т. е. можно считать две нормальные формы равными, если возможно α-преобразование одной в другую).

Поэтому и сильно нормализующие члены, и слабо налаживающие понятия имеют единственную нормальную форму. Для первых терминов любая стратегия сокращения гарантированно приведет к типичной конфигурации. Тогда как для слабо нормализующих условий некоторые стратегии сокращения могут не найти ее.

Дополнительные методы программирования

Существует большое количество идиом создания для лямбда-исчисления. Многие из них были первоначально разработаны в контексте использования систем в качестве основы для семантики языка программирования, эффективно применяя их в качестве создания низкого уровня. Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.

Именованные константы

В лямбда-исчислении библиотека принимает форму набора ранее определенных функций, в которой термины являются просто конкретными константами. Чистое исчисление не имеет понятия именованных неизменных, поскольку все атомные лямбда-термины являются переменными. Но их также можно имитировать, выделив непостоянную в качестве имени константы, используя лямбда-абстракцию для связывания этой изменчивой в основной части, и применить эту абстракцию к намеченному определению. Таким образом, если использовать f для обозначения M в N, можно сказать,

Авторы часто вводят синтаксическое понятие, такое как let, чтобы разрешить писать все в более интуитивном порядке.

Заметным ограничением этого let является то, что имя f не определено в M, поскольку M находится вне области привязки лямбда-абстракции f. Это означает, что атрибут рекурсивной функции не может использоваться как M с let. Более продвинутая синтаксическая конструкция letrec, которая позволяет писать рекурсивные определения функций в этом стиле, вместо этого дополнительно использует комбинаторы с фиксированной точкой.

Печатные аналоги

Данный тип является типизированным формализмом, который использует символ для обозначения анонимной функции абстракция. В этом контексте типы обычно являются объектами синтаксической природы, которые присваиваются лямбда-терминам. Точная натура зависит от рассматриваемого исчисления. С определенной точки зрения, типизированные ЛИ можно рассматривать как уточнения нетипизированного ЛИ. Но с другой стороны, их также можно считать более фундаментальной теорией, а нетипизированное лямбда-исчисление — особым случаем только с одним типом.

Типизированные ЛИ являются основополагающими языками программирования и основой функциональных, таких как ML и Haskell. И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.

Типизированные лямбда-исчисления тесно связаны с математической логикой и теорией доказательств через изоморфизм Карри – Говарда, и их можно рассматривать как внутренний язык классов категорий, например, который просто является стилем декартовых замкнутых.

Во всех двигателях внутреннего сгорания сгорает смесь топлива с воздухом. Полное сгорание топлива получается при достаточном количестве воздуха. К одному грамму топлива надо подмешать 14,7 гр. воздуха, только в этом случае будет достаточно молекул кислорода.

Смесь может быть богатой, когда немного не хватает воздуха, но горит она хорошо и быстро. Часть топлива не сгорает и выбрасывается в виде дыма.

Смесь может быть бедной, если воздуха слишком много, сгорает все топливо, но горит такая смесь вяло.

Что такое Лямбда (λ), или, по Советской литературе, альфа (α)?

Это интересно, еcли интересно понять, что такое λ-зонд - датчик кислорода.

λ – это характеристика состава смеси. Если воздуха нормальное количество, то λ равна 1, если воздуха в смеси больше - смесь бедная, то λ больше 1, если воздуха меньше, смесь богатая, то λ меньше 1. Таким образом, если λ =1, то смесь нормальная.

Для увеличения мощности, которая зависит от скорости сгорания топлива, делают смесь богатой, она сгорает быстрее, но не полностью.

Для увеличения экономичности, смесь делают бедной, она сгорает медленнее, но полностью.

Однако, в современных двигателях смесь приходится делать нормального состава, это делается ради снижения вредных выбросов из выхлопной трубы.

Для уменьшения количества вредных примесей в выхлопных газах, в выхлопную трубу вставляют пористый керамический дожигатель, в нем сделано напыление микрослоя платины, платина – катализатор. (катализатор – вещество ускоряющее химические реакции) в присутствии платины вредные составляющие выхлопных газов почти полностью нейтрализуются и на выходе получается безвредные составляющие воздуха.

Такая вставка в выхлопную трубу называется "каталитический нейтрализатор", или просто говорят "катализатор"

Каталитический нейтрализатор выполняет свою функцию, только, если в цилиндре происходит сгорание смеси нормального состава λ =1. При бедной или богатой смеси, нейтрализатор работает неэффективно.

λ-зонд встроен в выхлопную трубу и показывает состав смеси. Если она богатая, инжектор обедняет ее до нормально состава, если она бедная, то инжектор обогащает ее до нормально состава. В результате, каталитический нейтрализатор постоянно работает эффективно, дожигая выхлопные газы до безвредного состава.

Поддержание состава смеси λ =1, в современных двигателях, ухудшает мощностные и экономические показатели двигателя ради достижения чистоты выхлопных газов.

Читайте также: