Закон лямбда b t открыли

Обновлено: 03.07.2024

Лямбда-исчисление (англ. lambda calculus) — формальная система, придуманная в 1930-х годах Алонзо Чёрчем. Лямбда-функция является, по сути, анонимной функцией. Эта концепция показала себя удобной и сейчас активно используется во многих языках программирования.

Содержание

[math] \Lambda \to V\\ \Lambda \to \Lambda \ \Lambda\\ \Lambda \to \lambda V . \Lambda [/math]

Пробел во втором правиле является терминалом грамматики. Иногда его обозначают как @, чтобы он не сливался с другими символами в выражении.

В первом случае функция является просто переменной. Во втором происходит аппликация (применение) одной функции к другой. Это аналогично вычислению функции-левого операнда на аргументе-правом операнде. В третьем — абстракция по переменной. В данном случае происходит создание функции одного аргумента с заданными именем аргумента и телом функции.

Рассмотрим, например, [math]\lambda[/math] -терм [math]\operatorname = \lambda x\ .\ x[/math] . Эта функция принимает аргумент и возвращает его неизменённым. Например, [math]\operatorname\ 2 \equiv 2[/math] . Аналогично, [math]\operatorname\ y \equiv y[/math] .

[math] x\\ (x\ z)\\ (\lambda x.(x\ z))\\ (\lambda z.(\lambda w.((\lambda y.((\lambda x.(x\ z))\ y))\ w)))\\ [/math]

Иногда [math]\lambda[/math] -термы пишут по другому. Для краткости подряд идущие лямбды заменяют на одну. Например:

[math]\lambda x\ .\ \lambda y\ .P\ \to\ \lambda xy.P[/math]

Аппликация: [math]x\ y\ z\ w \equiv ((x\ y)\ z)\ w[/math]
Абстракция забирает себе всё, до чего дотянется: [math]\lambda x\ .\ \lambda y\ .\ \lambda z\ .\ z\ y\ x \equiv \lambda x\ .\ (\lambda y\ .\ (\lambda z\ .\ ((z\ y)\ x)))[/math]
Скобки играют привычную роль группировки действий

Связанными переменными называются все переменные, по которым выше в дереве разбора были абстракции. Все остальные переменные называются свободными.

Например, в [math]\lambda x\ .\ y\ x[/math] , [math]x[/math] и связана, а [math]y[/math] — свободна. А в [math]\lambda y\ .\ x\ (\lambda x\ .\ x)[/math] в своём первом вхождении переменная [math]x[/math] свободна, а во втором — связана.

Связанные переменные — это аргументы функции. То есть для функции они являются локальными.

Рассмотрим функции [math]\lambda y\ .\ y[/math] и [math]\lambda x\ .\ y[/math] . В первой из них при взгляде на [math]y[/math] понятно, что она имеет отношение к переменной, по которой производилась абстракция. Если по одной и той же переменной абстракция производилась более одного раза, то переменная связана с самым поздним (самым нижним в дереве разбора) абстрагированием. Например, в [math]\lambda x\ .\ \lambda x\ .\ \lambda y\ .\ \lambda x\ .\ x[/math] , переменная [math]x[/math] связана с самой правой абстракцией по [math]x[/math] .

и замкнуто относительно следующих правил:

Функции [math]\lambda x\ .\ \lambda y\ .\ x\ y\ z[/math] и [math]\lambda a\ .\ \lambda x\ .\ a\ x\ z[/math] являются [math]\alpha[/math] -эквивалентными, а [math]\lambda x\ .\ \lambda y\ .\ y\ z[/math] и [math]\lambda y\ .\ \lambda x\ .\ y\ z[/math] — нет.

и замкнуто относительно следующих правил

В [math]\beta[/math] -редукции вполне возможна функция вида [math]\lambda x. \lambda x.x[/math] . Во время подстановки вместо [math]x[/math] внутренняя переменная не заменяется - действует принцип локальной переменной. Но принято считать, что таких ситуаций не возникает и все переменные называются разными именами.

Существует также альтернативное эквивалентное определение [math]\lambda[/math] -исчисления. В оригинальном определении для обозначения переменных использовались имена, и была проблема с тем, что не были запрещены одинаковые имена в разных абстракциях.

От этой проблемы можно избавиться следующим образом. Вместо имени переменной будет храниться натуральное число — количество абстракций в дереве разбора, на которое нужно подняться, чтобы найти ту лямбду, с которой данная переменная связана. В данной нотации получаются несколько более простые определения свободных переменных и [math]\beta[/math] -редукции.

Грамматику нотации можно задать как:

[math]e\ ::= n\ |\ \lambda .e\ |\ e\ e[/math]

Примеры выражений в этой нотации:

Standart	de Bruijn
$\lambda x.x$	$\lambda .0$
$\lambda z.z$	$\lambda .0$
$\lambda x. \lambda y.x$	$\lambda . \lambda .1$
$\lambda x. \lambda y. \lambda s. \lambda z.x\ s\ (y\ s\ z)$	$\lambda . \lambda . \lambda . \lambda .3\ 1(2\ 1\ 0)$
$(\lambda x.x\ x)(\lambda x.x\ x)$	$(\lambda .0\ 0)(\lambda .0\ 0)$
$(\lambda x. \lambda x.x)(\lambda y.y)$	$(\lambda .\lambda .0)(\lambda .0)$

Переменная называется свободной, если ей соответствует число, которое больше количества абстракций на пути до неё в дереве разбора.

Введём на основе лямбда-исчисления аналог натуральных чисел, основанный на идее, что натуральное число — это или ноль, или увеличенное на единицу натуральное число.

[math]\bar 0 = \lambda s\ .\ \lambda z\ .\ z[/math] [math]\bar 1 = \lambda s\ .\ \lambda z\ .\ s\ z[/math] [math]\bar 2 = \lambda s\ .\ \lambda z\ .\ s\ (s\ z)[/math] [math]\bar 3 = \lambda s\ .\ \lambda z\ .\ s\ (s\ (s\ z))[/math]

Каждое число будет функцией двух аргументов: какой-то функции и начального значения. Число [math]n[/math] будет [math]n[/math] раз применять функцию к начальному значению и возвращать результат. Если такому "числу" дать на вход функцию [math](+1)[/math] и [math]0[/math] в качестве начального значения, то на выходе как раз будет ожидаемое от функции число: [math]\bar 3\ (+1)\ 0 \equiv 3[/math] .

Функция, прибавляющая [math]1[/math] к числу, должна принимать первым аргументом число. Но число — функция двух аргументов. Значит, эта функция должна принимать три аргумента: "число" [math]n[/math] , которое хочется увеличить, функция, которую надо будет [math]n+1[/math] раз применить, и начальное значение.

[math]\operatorname = \lambda n\ .\ \lambda s\ .\ \lambda z\ .\ s\ (n\ s\ z)[/math]

Здесь [math]n\ s\ z[/math] — [math]n[/math] раз применённая к [math]z[/math] функция [math]s[/math] . Но нужно применить [math]n+1[/math] раз. Отсюда [math]s\ (n\ s\ z)[/math] .

Сложение двух чисел похоже на прибавление единицы. Но только надо прибавить не единицу, а второе число.

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \lambda s\ .\ \lambda z\ .\ n\ s\ (m\ s\ z)[/math]

[math]n[/math] раз применить [math]s[/math] к применённому [math]m[/math] раз [math]s[/math] к [math]z[/math]

[math](\operatorname\ \bar 3\ \bar 3)\ (+1)\ 0 \equiv 6[/math]

[math](\operatorname\ ((\operatorname\ 2\ 5)(+1)\ 0)\ 4)(+1)0 \equiv 11[/math]

Умножение похоже на сложение, но прибавлять надо не единицу, а второе число. Или, в терминах нумералов Чёрча, в качестве применяемой несколько раз функции должна быть не [math]s[/math] , а функция, применяющая [math]n[/math] раз [math]s[/math] .

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \lambda s\ .\ \lambda z\ .\ n\ (m\ s)\ z[/math]

Здесь [math]m\ s[/math] — функция, которая [math]m[/math] раз применит [math]s[/math] к тому, что дадут ей на вход. С помощью [math]\eta[/math] -редукции можно немного сократить эту формулу

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \lambda s\ .\ n\ (m\ s)[/math]

[math](\operatorname \bar 3\ \bar 3)\ (+1)\ 0 \equiv 9[/math]

It's a kind of magic

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \lambda s\ .\ \lambda z\ .\ m\ n\ s\ z[/math]

[math](\operatorname\ \bar 3\ (\operatorname\ \bar 3))\ (+1)\ 0 \equiv 81[/math]

[math]\operatorname = \lambda a\ .\ \lambda b\ .\ a[/math]

[math]\operatorname = \lambda a\ .\ \lambda b\ .\ b[/math]

Функции двух аргументов, возвращающие первый и второй, соответственное, аргументы. Забавный факт: [math]\operatorname \equiv_\alpha \operatorname[/math] . Эти функции сделаны такими для того, чтобы красиво написать функцию [math]\operatorname[/math] :

[math]\operatorname = \lambda p\ .\ \lambda t\ .\ \lambda e\ .\ p\ t\ e[/math]

Если ей в качестве первого аргумента дадут [math]\operatorname[/math] , то вернётся [math]t[/math] , иначе — [math]e[/math] .

Стандартные функции булевой логики:

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ n\ m\ \operatorname[/math]

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ n\ \operatorname \ m[/math]

[math]\operatorname = \lambda b\ .\ \operatorname\ b\ \operatorname \ \operatorname[/math]

Ещё одной важной функцией является функция проверки, является ли число нулём:

[math]\operatorname = \lambda n\ .\ n\ (\lambda c\ .\ \operatorname)\ \operatorname[/math]

Функция выглядит несколько странно. [math]\lambda c \to \operatorname[/math] - функция, которая независимо от того, что ей дали на вход, возвращает [math]\operatorname[/math] . Тогда, если в качестве [math]n[/math] будет дан ноль, то функция, по определению нуля, не выполнится ни разу, и будет возвращено значение по умолчанию [math]\operatorname[/math] . Иначе же функция будет запущено, и вернётся [math]\operatorname[/math] .

[math]\operatorname = \lambda a\ .\ \lambda b\ .\ \lambda t\ .\ t\ a\ b[/math]

[math]\operatorname = \lambda p\ .\ p\ \operatorname[/math]

Функция [math]\operatorname[/math] принимает два значения и запаковывает их в пару так, чтобы к ним можно было обращаться по [math]\operatorname[/math] и [math]\operatorname[/math] . В [math]\operatorname[/math] и [math]\operatorname[/math] вместо [math]t[/math] в [math]\operatorname[/math] будет подставлено [math]\operatorname[/math] или [math]\operatorname[/math] , возвращающие, соответственно, первый и второй аргументы, то есть [math]a[/math] или [math]b[/math] , соответственно.

В отличие от всех предыдущих функций, вычитание для натуральных чисел определено только в случае, если уменьшаемое больше вычитаемого. Положим в противном случае результат равным нулю. Пусть уже есть функция, которая вычитает из числа единицу. Тогда на её основе легко сделать, собственно, вычитание.

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ m\ \operatorname n[/math]

Это то же самое, что [math]m[/math] раз вычесть единицу из [math]n[/math] .

Осталось, собственно, функция для вычитания единицы. Однако, это не так просто, как может показаться на первый взгляд. Проблема в том, что, имея функцию, которую нужно применить для того, чтобы продвинуться вперёд, продвинуться назад будет проблематично. Если попробовать воспользоваться идеей о том, чтобы, начав от нуля, идти вперёд, и пройти на один шаг меньше, то будет не очень понятно, как же остановиться ровно за один шаг до конца. Для реализации вычитания единицы сделаем следующее. [math]n[/math] раз выполним следующее: имея пару [math]\langle n-1, n-2\rangle[/math] построим пару [math]\langle n, n-1\rangle[/math] . Тогда после [math]n[/math] шагов во втором элементе пары будет записано число [math]n-1[/math] , которое и хочется получить.

[math]\operatorname = \lambda n\ .\ \lambda s\ .\ \lambda z.\ \operatorname\ ( n\ ( \lambda p\ .\ \operatorname\ (s\ (\operatorname p))\ (\operatorname p) )\ (\operatorname\ z\ z))[/math]

Если вы ничего не поняли, не огорчайтесь. Вычитание придумал Клини, когда ему вырывали зуб мудрости. А сейчас наркоз уже не тот.

Так как вычитание определено таким способом, чтобы для случая, в котором уменьшаемое больше, чем вычитаемое, возвращать ноль, можно определить сравнение на больше-меньше через него. Равными же числа [math]a[/math] и [math]b[/math] считаются, если [math]a - b = 0 \wedge b - a = 0[/math] .

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ n\ m)[/math]

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ n\ (\operatorname m)[/math]

[math]\operatorname = \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ (\operatorname\ n\ m))\ (\operatorname\ (\operatorname\ m\ n))[/math]

Попробуем выразить в лямбда-исчислении какую-нибудь функцию, использующую рекурсию. Например, факториал.

[math]\operatorname = \lambda x\ .\ \operatorname\ (\operatorname\ x)\ \bar 1\ (\operatorname\ (\operatorname\ x))[/math]

Мы столкнулись с проблемой. В определении функции [math]\operatorname[/math] используется функция [math]\operatorname[/math] . При формальной замене, получим бесконечную функцию. Можно попытаться решить эту проблему следующим образом

[math]\operatorname = (\lambda f\ .\ \lambda x\ .\ \operatorname\ (\operatorname\ x)\ \bar 1\ (f\ (\operatorname\ x)))\ \operatorname[/math]

Лямбда исчисление обладаем замечательным свойством: у каждой функции есть неподвижная точка!

Рассмотрим следующую функцию.

[math]\operatorname = \lambda f\ .\ (\lambda x\ .\ f\ (x\ x))\ (\lambda x\ .\ f\ (x\ x))[/math]

Заметим, что [math]\operatorname \to_\beta^* \lambda f\ .\ f\ ((\lambda x\ .\ f\ (x\ x))\ (\lambda x\ .\ f\ (x\ x)))[/math] . Или, что то же самое, [math]\lambda f\ .\ (\lambda x\ .\ f\ (x\ x))\ (\lambda x\ .\ f\ (x\ x)) \to_\beta^*[/math] [math]\lambda f\ .\ f\ ((\lambda x\ .\ f\ (x\ x))\ (\lambda x\ .\ f\ (x\ x)))[/math]

[math]\operatorname = \lambda f\ .\ \lambda x\ .\ \operatorname\ (\operatorname\ x)\ \bar 1\ (\operatorname\ x\ (f\ (\operatorname\ x)))[/math]

Как было показано выше, [math]\operatorname f \to_\beta^* f\ (\operatorname f)[/math] , то есть, [math]\operatorname\ \operatorname \to_\beta^* \operatorname[/math] , где [math]\operatorname[/math] — искомая функция, считающая факториал.

[math]\operatorname = \operatorname\ \operatorname[/math]

Это даст функцию, которая посчитает факториал числа. Но делать она это будет мееедленно-меееедленно. Для того, чтобы посчитать [math]5![/math] потребовалось сделать 66066 [math]\beta[/math] -редукций.

Наиболее известным комбинатором неподвижной точки является [math]Y[/math] -комбинатор, введенный известным американским ученым Хаскеллом Карри как

[math]Y\ = \ \lambda f.(\lambda x.f(x\ x))\ (\lambda x.f(x\ x))[/math]

Воспользовавшись идеей о том, что можно делать рекурсивные функции, сделаем функцию, которая будет искать частное двух чисел.

[math]\operatorname = \lambda div\ .\ \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ n\ m)\ \bar 0\ (\operatorname\ (div\ (\operatorname\ n\ m)\ m))[/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

И остатка от деления

[math]\operatorname = \lambda mod\ .\ \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ n\ m)\ n\ (mod\ (\operatorname\ n\ m)\ m)[/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

[math]\operatorname[/math] — принимает число, которое требуется проверить на простоту и то, на что его надо опытаться поделить, перебирая это от [math]2[/math] до [math]p-1[/math] . Если на что-нибудь разделилось, то число — составное, иначе — простое.

[math]\operatorname =[/math] [math]\lambda f\ .\ \lambda p\ .\ \lambda i\ .\ \operatorname\ (\operatorname\ p\ i)\ \operatorname\ (\operatorname\ (\operatorname\ (\operatorname\ p\ i))\ \operatorname\ (f\ p\ (\operatorname\ i)))[/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

[math]\operatorname = \lambda p\ .\ \operatorname\ p\ \bar 2[/math]

Следующее простое число. [math]\operatorname[/math] — следующее, больше либо равное заданного, [math]\operatorname[/math] — следующее, большее заданного.

[math]\operatorname = \lambda f\ .\ \lambda p\ .\ \operatorname\ (\operatorname\ p)\ p\ (f\ (\operatorname\ p)) [/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

[math]\operatorname = \lambda p\ .\ \operatorname\ (\operatorname\ p)[/math]

[math]\operatorname[/math] пропрыгает [math]i[/math] простых чисел вперёд. [math]\operatorname[/math] принимает число [math]i[/math] и пропрыгивает столько простых чисел вперёд, начиная с двойки.

[math]\operatorname = \lambda f\ .\ \lambda p\ .\ \lambda i\ .\ \operatorname\ (\operatorname\ i)\ p\ (f\ (\operatorname\ p)\ (\operatorname\ i))[/math]

[math]\operatorname = \lambda i\ .\ \operatorname\ \bar 2\ i[/math]

. и всего через 314007 [math]\beta[/math] -редукций вы узнаете, что третье простое число — семь!

Для работы со списками чисел нам понадобятся следующие функции:

[math]\operatorname[/math] — возвращает пустой список
[math]\operatorname[/math] — принимает первый элемент и оставшийся список, склеивает их
[math]\operatorname[/math] — вернуть голову списка
[math]\operatorname[/math] — вернуть хвост списка

[math]\operatorname = \operatorname\ \operatorname\ \bar 1[/math]

[math]\operatorname = \lambda h\ .\ \lambda t\ .\ \operatorname\ (\operatorname\ (\operatorname\ t))\ (\operatorname\ (\operatorname\ t)\ (\operatorname\ (\operatorname\ (\operatorname\ t))\ h))[/math]

[math]\operatorname = \lambda list\ .\ \operatorname\ (\operatorname\ list)\ (\operatorname\ (\operatorname\ (\operatorname\ list)))[/math]

[math]\operatorname = \lambda list\ .\ \operatorname\ (\operatorname\ (\operatorname\ list)) (\operatorname\ (\operatorname\ list)\ (\operatorname\ (\operatorname\ (\operatorname\ list))))[/math]

[math]\operatorname =[/math] [math] \lambda f\ .\ \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ (\operatorname\ n\ m))\ (f\ (\operatorname\ n\ m)\ m)\ n[/math]

[math]\operatorname =[/math] [math] \lambda f\ .\ \lambda n\ .\ \lambda m\ .\ \operatorname\ (\operatorname\ (\operatorname\ n\ m))\ (\operatorname\ (f\ (\operatorname\ n\ m)\ m))\ \bar 0[/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

Лямбда-исчисление — это формальная система в математической логике для выражения подсчетов на основе абстракции и применения функций с использованием привязки и подстановки переменных. Это универсальная модель, которую можно применять для проектирования любой машины Тьюринга. Впервые введена лямбда-исчисления Черчем, известным математиком, в 1930-х годах.

Система состоит из построения лямбда-членов и выполнения над ними операций сокращения.

Пояснения и приложения

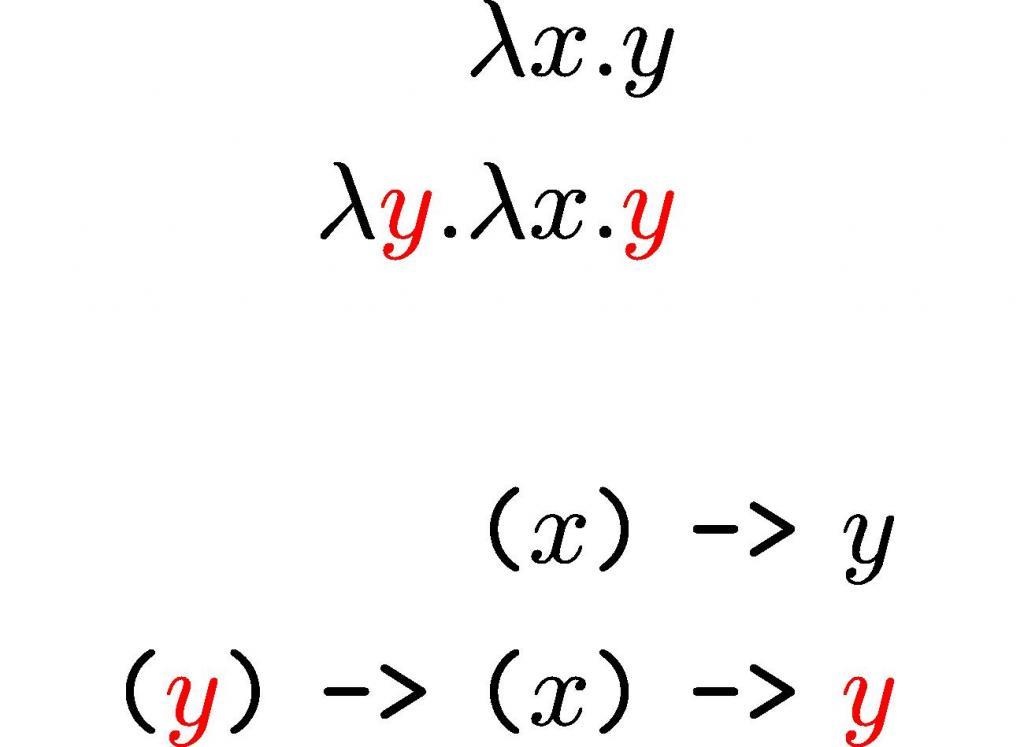
Вам будет интересно: Какие элементы входят в социальную структуру общества, виды и функции социальных групп

Греческая буква lambda (λ) используется в лямбда-выражениях и лямбда-терминах для обозначения связывания переменной в функции.

Лямбда-исчисление может быть нетипизировано или напечатано. В первом варианте функции могут быть применены только в том случае, если они способны принимать данные этого типа. Типизированные лямбда-исчисления слабее, могут выражать меньшее значение. Но, с другой стороны, они позволяют доказывать больше вещей.

Одной из причин того, что существует много разных типов — это желание ученых сделать больше, не отказываясь от возможности доказывать сильные теоремы лямбда-исчислений.

Вам будет интересно: Семейный этикет: основы и правила, особенности отношений с близкими родственниками

Система находит применение во многих различных областях математики, философии, лингвистики, и компьютерных наук. В первую очередь, лямбда-исчисления — это расчет, который сыграл важную роль в развитии теории языков программирования. Именно стили функционального создания реализуют системы. Они также являются актуальной темой исследований в теории этих категорий.

Для чайников

Лямбда-исчисление была введена математиком Алонзо Черчем в 1930-х годах в рамках исследования основ науки. Первоначальная система была показана как логически несовместимая в 1935 году, когда Стивен Клин и Дж. Б. Россер разработали парадокс Клини-Россера.

В последствии, в 1936 году Черч выделил и опубликовал только ту часть, которая имеет отношение к расчетам, то, что сейчас называется нетипизированным лямбда-исчислением. В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.

Вам будет интересно: Профессии железнодорожников: перечень, описание, необходимое образование

До 1960-х годов, когда выяснилось его отношение к языкам программирования, λ стала лишь формализмом. Благодаря применениям Ричарда Монтегю и других лингвистов в семантике естественного языка, исчисление стало занимать почетное место как в лингвистике, так и в информатике.

Происхождение символа

Введение в лямбда исчисление

Система состоит из языка терминов, которые выбираются определенным формальным синтаксисом, и набора правил преобразования, которые позволяют манипулировать ими. Последний пункт можно рассматривать как эквациональную теорию или как операционное определение.

Все функции в лямбда-исчислении являются анонимными, то есть не имеющими имен. Они принимают только одну входную переменную, при этом каррирование используется для реализации графиков с несколькими непостоянными.

Лямбда-термины

Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически допустимых понятий:

Переменная x сама по себе является действительным лямбда-термином:

если T это ЛТ, и x непостоянная, то (lambda xt) называется абстракцией.
если T, а также s понятия, то (TS) называется приложением.

Ничто другое не является лямбда-термином. Таким образом, понятие действительно тогда и только тогда, когда оно может быть получено повторным применением этих трех правил. Тем не менее некоторые скобки могут быть опущены в соответствии с другими критериями.

Определение

Вам будет интересно: Виды контроля качества продукции при производстве

Лямбда-выражения состоят из:

переменных v 1, v 2. v n.
символов абстракции 'λ' и точки '.'
скобок ().

Множество Λ, может быть определено индуктивно:

Если x переменная, то x ∈ Λ;
x непостоянная и M ∈ Λ, то (λx.M) ∈ Λ;
M, N ∈ Λ, то (MN) ∈ Λ.

Обозначение

Чтобы сохранить нотацию лямбда-выражений в незагроможденном виде, обычно применяются следующие соглашения:

Внешние скобки опущены: MN вместо (MN).
Предполагается, что приложения остаются ассоциативными: взамен ((MN) P) можно написать MNP.
Тело абстракции простирается дальше вправо: λx.MN означает λx. (MN), а не (λx.M) N.
Сокращается последовательность абстракций: λx.λy.λz.N можно λxyz.N.

Свободные и связанные переменные

Оператор λ соединяет свою непостоянную, где бы он ни находился в теле абстракции. Переменные, попадающие в область, называются связанными. В выражении λ x. М, часть λ х часто называют связующим. Как бы намекая, что переменные становятся группой с добавлением Х х к М. Все остальные неустойчивые называются свободными.

Множество свободных переменных M обозначается как FV (M) и определяется рекурсией по структуре терминов следующим образом:

FV (x) = , где x - переменная.
FV (λx.M) = FV (M) .
FV (MN) = FV (M) ∪ FV (N).

Формула, которая не содержит свободных переменных, называется закрытой. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны терминам в комбинаторной логике.

Сокращение

Значение лямбда-выражений определяется тем, как они могут быть сокращены.

Существует три вида урезания:

α-преобразование: изменение связанных переменных (альфа).
β-редукция: применение функций к своим аргументам (бета).
η-преобразование: охватывает понятие экстенсиональности.

Здесь речь также идет о полученных эквивалентностях: два выражения являются β-эквивалентными, если они могут быть β-преобразованы в одно и то же составляющее, а α / η-эквивалентность определяется аналогично.

Термин redex, сокращение от приводимого оборота, относится к подтемам, которые могут быть сокращены одним из правил. Лямбда исчисление для чайников, примеры:

(λ x.M) N является бета-редексом в выражении замены N на x в M. Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].

Если x не является свободной в M, λ х. М х также ет-REDEX с регулятором М.

α-преобразование

Альфа-переименования позволяют изменять имена связанных переменных. Например, λ x. х может дать λ у. у. Термины, которые отличаются только альфа-преобразованием, называются α-эквивалентными. Часто при использовании лямбда-исчисления α-эквивалентные считаются взаимными.

Точные правила для альфа-преобразования не совсем тривиальны. Во-первых, при данной абстракции переименовываются только те переменные, которые связаны с одной и той же системой. Например, альфа-преобразование λ x.λ x. x может привести к λ y.λ x. х, но это может не ввергнуть к λy.λx.y Последний имеет иной смысл, чем оригинал. Это аналогично понятию программирования затенения переменных.

Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату непостоянной другой абстракцией. Например, если заменить x на y в λ x.λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.

В языках программирования со статической областью видимости альфа-преобразование можно использовать для упрощения разрешения имен. При этом следя за тем, чтобы понятие переменной не маскировало обозначение в содержащей области.

В нотации индекса Де Брюйна любые два альфа-эквивалентных термина синтаксически идентичны.

Замена

Изменения, написанные Е [V: = R], представляют собой процесс замещения всех свободных вхождений переменной V в выражении Е с оборотом R. Подстановка в терминах λ определяется лямбдой исчисления рекурсии по структуре понятий следующим образом (примечание: x и y - только переменные, а M и N - любое λ-выражение).

y [x: = N] ≡ y, если x ≠ y

(M 1 M 2) [x: = N] ≡ (M 1 [x: = N]) (M 2 [x: = N])

(λ x.M) [x: = N] ≡ λ x.M

(λ y.M) [x: = N] y λ y. (M [x: = N]), если x ≠ y, при условии, что y ∉ FV (N).

Для подстановки в лямбда-абстракцию иногда необходимо α-преобразовать выражение. Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.

β-редукция

Бета-редукция отражает идею применения функции. Бета-восстановительный определяется в терминах замещения: ((X V. E) Е ') является Е [V: = Е'].

Например, предполагая некоторое кодирование 2, 7, ×, имеется следующее β-уменьшение: ((λ n. N × 2) 7) → 7 × 2.

Бета-редукция может рассматриваться как то же самое, что и концепция локальной сводимости при естественной дедукции через изоморфизм Карри – Ховарда.

η-преобразование

Эта-конверсия выражает идею экстенсиональности, которая в этом контексте заключается в том, что две функции равны тогда, когда они дают одинаковый результат для всех аргументов. Эта конвертация обменивает между λ x. (F x) и f всякий раз, когда x не кажется свободным в f.

Вам будет интересно: Откуда появились славяне: определение, описание и история

Данное действие может рассматриваться как то же самое, что и концепция локальной полноты в естественной дедукции через изоморфизм Карри – Ховарда.

Нормальные формы и слияние

Для нетипизированного лямбда-исчисления β-редукция как правило переписывания не является ни сильно нормализующей, ни слабо.

Тем не менее можно показать, что β-редукция сливается при работе до α-преобразования (т. е. можно считать две нормальные формы равными, если возможно α-преобразование одной в другую).

Поэтому и сильно нормализующие члены, и слабо налаживающие понятия имеют единственную нормальную форму. Для первых терминов любая стратегия сокращения гарантированно приведет к типичной конфигурации. Тогда как для слабо нормализующих условий некоторые стратегии сокращения могут не найти ее.

Дополнительные методы программирования

Существует большое количество идиом создания для лямбда-исчисления. Многие из них были первоначально разработаны в контексте использования систем в качестве основы для семантики языка программирования, эффективно применяя их в качестве создания низкого уровня. Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.

Именованные константы

В лямбда-исчислении библиотека принимает форму набора ранее определенных функций, в которой термины являются просто конкретными константами. Чистое исчисление не имеет понятия именованных неизменных, поскольку все атомные лямбда-термины являются переменными. Но их также можно имитировать, выделив непостоянную в качестве имени константы, используя лямбда-абстракцию для связывания этой изменчивой в основной части, и применить эту абстракцию к намеченному определению. Таким образом, если использовать f для обозначения M в N, можно сказать,

Авторы часто вводят синтаксическое понятие, такое как let, чтобы разрешить писать все в более интуитивном порядке.

Заметным ограничением этого let является то, что имя f не определено в M, поскольку M находится вне области привязки лямбда-абстракции f. Это означает, что атрибут рекурсивной функции не может использоваться как M с let. Более продвинутая синтаксическая конструкция letrec, которая позволяет писать рекурсивные определения функций в этом стиле, вместо этого дополнительно использует комбинаторы с фиксированной точкой.

Печатные аналоги

Данный тип является типизированным формализмом, который использует символ для обозначения анонимной функции абстракция. В этом контексте типы обычно являются объектами синтаксической природы, которые присваиваются лямбда-терминам. Точная натура зависит от рассматриваемого исчисления. С определенной точки зрения, типизированные ЛИ можно рассматривать как уточнения нетипизированного ЛИ. Но с другой стороны, их также можно считать более фундаментальной теорией, а нетипизированное лямбда-исчисление — особым случаем только с одним типом.

Типизированные ЛИ являются основополагающими языками программирования и основой функциональных, таких как ML и Haskell. И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.

Типизированные лямбда-исчисления тесно связаны с математической логикой и теорией доказательств через изоморфизм Карри – Говарда, и их можно рассматривать как внутренний язык классов категорий, например, который просто является стилем декартовых замкнутых.

Многие задаются вопросом зачем он вообще нужен, и зачастую наслушавшись безграмотных советов доморощенных *чиптюнеров* стремятся его разными способами удалить из системы. Не буду долго лить всякую теоретическую воду напишу кратко:
-для владельца авто он позволяет экономить бензин как гласит запись из каталога бош (см. рис.) при исправном двигателе, системе управления ну и собственно лямбда зонде (далее ЛЗ) это реальная экономия до 15% топлива, нетрудно посчитать это 1,5 л на 10 л!

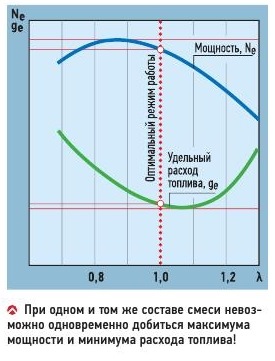
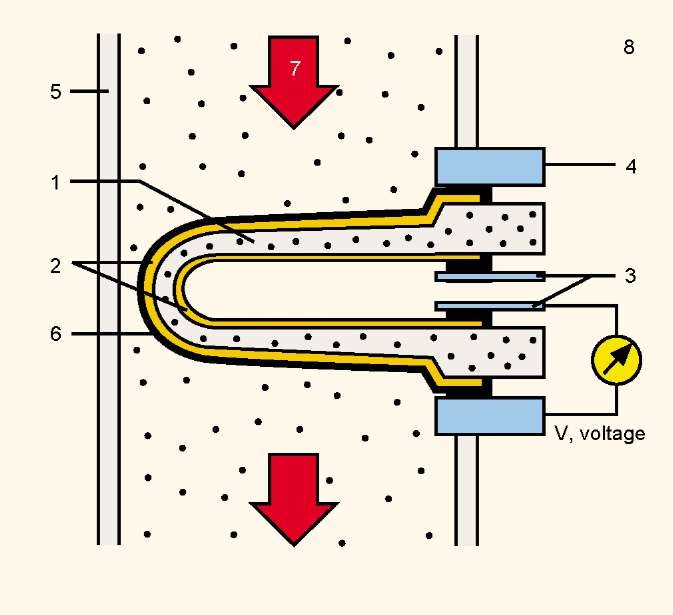
Рисунок 3. Датчик кислорода в выхлопной трубе
1. Керамическое покрытие
2. Электроды
3. Контакты
4. контакты корпуса
5. Выхлопная труба
6. Керамическая поддерживающая оболочка (пористая)
7. Отработавшие газы
8. Наружный воздух.

Датчик кислорода представляет собой гальваническую ячейку (ячейку Нернста) с твёрдым электролитом. В качестве электролита используется газонепроницаемая керамика из диоксида циркония (ZrO2), стабилизированного оксидом иттрия (YO). C одной стороны (снаружи) он сообщается с выхлопными газами, а с другой (изнутри) — с атмосферой. На внешнюю и внутреннюю сторону керамики нанесены газопроницаемые электроды из тонкого слоя платины.
Платиновый электрод на наружной стороне работает как миниатюрный катализатор, поддерживающий в прилегающем слое поступающих выхлопных газов химические реакции, этот слой в состояние стехиометрического равновесия. Сторона чувствительной керамики, обращенная к отработавшим газам, во избежание ее загрязнения покрыта слоем пористой шпинелевой керамики (Шпинель — минералогическое название тетраоксида диалюминия-магния). Металлическая трубка со щелями предохраняет керамику от ударов и чрезмерных тепловых воздействий. Внутренняя полость сообщается с атмосферой и служит в качестве референсной (опорной) стороны датчика.
Работа датчика основана на принципе ячейки Нернста (гальванической ячейки). Керамический материал пропускает ионы кислорода при температурах от 350oC и выше. Разница в количестве кислорода с разных сторон чувствительной зоны датчика приводит к образованию электрического потенциала (напряжения) между этими двумя поверхностями (внутренней и внешней). Величина напряжения служит показателем того, на сколько количество кислорода на этих двух поверхностях различается. А количество остаточного кислорода в выхлопных газах точно соответствует пропорции между топливом и воздухом, поступающими в двигатель.
Широкополосный λ-датчик кислорода

Рисунок . Конструкция широкополосного датчика кислорода непрерывного действия, установленного в выхлопной трубе.
1. Ячейка Нернста
2. Референсная ячейка
3. Подогреватель
4. Диффузионная щель
5. Насосная ячейка
6. Выхлопная труба
Эта конфигурация отличается от обычного датчика с двумя состояниями постоянным поддержанием стехиометрического соотношением воздух/топливо в диффузионной камере. Электронная схема модуляции напряжения питания поддерживает в измерительной камере состав газов, соответствующий λ=1. Для этого насосная ячейка при работе двигателя на бедной смеси и избытке кислорода в выхлопных газах удаляет кислород из диффузионной щели во внешнюю среду; а при богатой смеси и недостатке кислорода в выхлопных газах перекачивает ионы кислорода из окружающей среды в диффузионную щель. Направление тока для перекачивания кислорода в разные стороны тоже отличается.
Так как насосный ток пропорционален концентрации кислорода — он и является показателем величины λ-фактора отработавших газов.

Таким образом, если обычные датчики используют напряжение на ячейке Нернста для прямого измерения и определения одного из двух состояний (λ>1 или λ

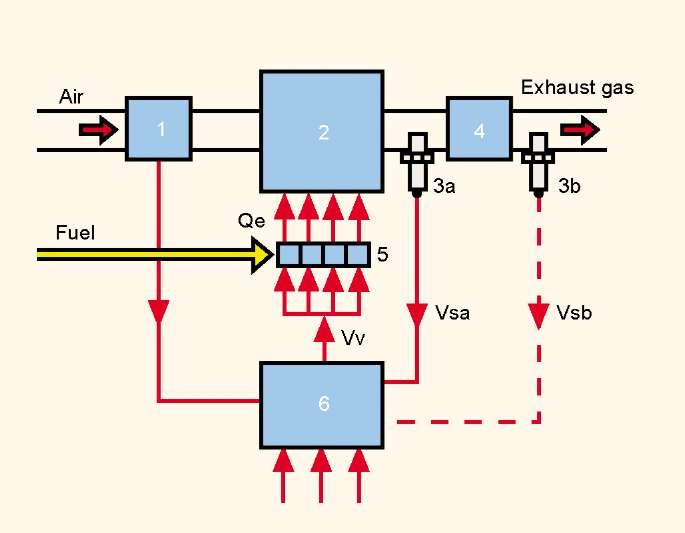
Рисунок . Схема замкнутой петли λ-регулирования качества смеси.
1. Датчик массового расхода воздуха
2. Двигатель
3a. Датчик кислорода 1
3b. Датчик кислорода 2
4. Катализатор
5. Форсунки инжектора
6. Электронный Блок Управления
Vv напряжение управления форсунками
Vs напряжение с датчика
Qe Количество впрыскиваемого топлива
Датчик кислорода передает сигнал (напряжение) электронному блоку управления (ЭБУ) двигателем. Этот сигнал используется системой для обогащения или обеднения смеси в соответствии с величиной напряжения с датчика (см. Рис. 8). Таким образом система обогащает бедную смесь, увеличивая количество впрыскиваемого топлива, и обедняет богатую, уменьшая количество топлива.
Диагностика
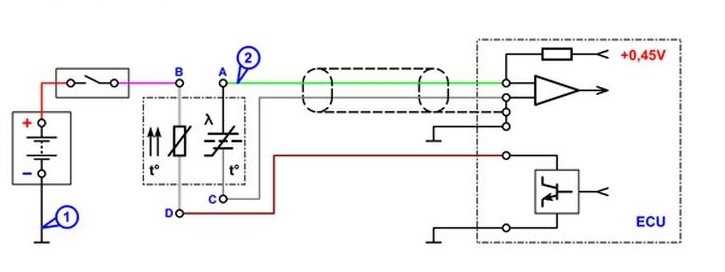
Лямбда-зонд сравнивает уровень содержания кислорода в выхлопных газах и в окружающем воздухе и представляет результат этого сравнения в форме аналогового сигнала. Применяются двухуровневые зонды, чувствительный элемент которых выполнен из оксида циркония либо из оксида титана, но на их смену приходят широкополосные лямбда-зонды. При условии сгорания стехиометрической топливо-воздушной смеси, напряжение выходного сигнала лямбда-зонда равно 445…450mV.

Но расстояние от выпускных клапанов газораспределительного механизма двигателя до места расположения датчика и значительное время реакции чувствительного элемента датчика приводят к некоторой инерционности системы, что не позволяет непрерывно поддерживать стехиометрический состав топливо-воздушной смеси. Практически, при работе двигателя на установившемся режиме, состав смеси постоянно отклоняется от стехиометрического в диапазоне ±2…3% с частотой 1…2раза в секунду. Этот процесс чётко прослеживается по осциллограмме напряжения выходного сигнала лямбда-зонда.

осциллограмма напряжения выходного сигнала исправного лямбда-зонда BOSCH.

Двигатель работает на холостом ходу. Частота переключения сигнала составляет ~1,2Hz.

Осциллограмма напряжения выходного сигнала неисправного лямбда-зонда BOSCH.

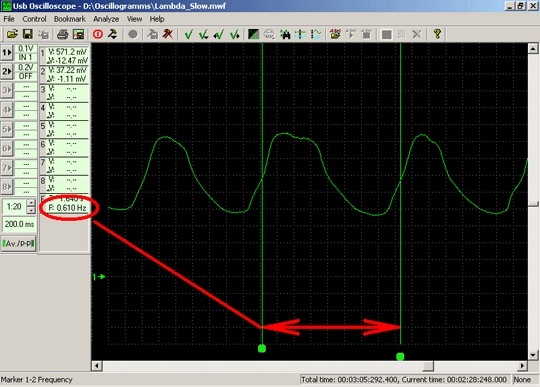
Осциллограмма напряжения выходного сигнала неисправного лямбда-зонда BOSCH. Двигатель работает на холостом ходу. Переключения выходного сигнала отсутствуют. Напряжение выходного сигнала стареющего лямбда-зонда при работе двигателя на холостом ходу становится почти стабильным, его значение становится близким опорному напряжению 300…600mV.

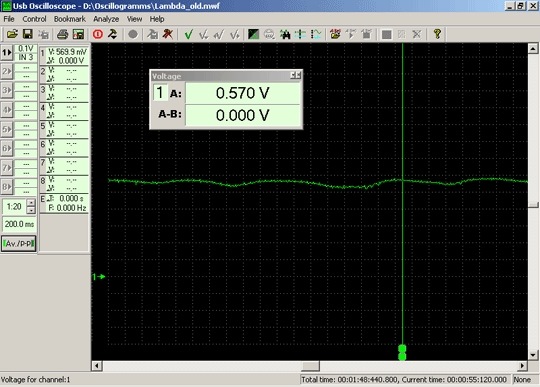
Уровень содержания кислорода в камере с атмосферным воздухом при этом оказывается значительно выше уровня содержания кислорода в выхлопных газах, вследствие чего зонд генерирует напряжение 1V положительной полярности. В случае разгерметизации лямбда-зонда, в камеру с атмосферным воздухом проникают отработавшие газы с низким содержанием кислорода. На режиме торможения двигателем (закрытая дроссельная заслонка при вращении двигателя с высокой частотой, подача топлива при этом отключена), в выхлопную систему двигателем выбрасывается почти чистый атмосферный воздух. В таком случае, уровень содержания кислорода в выхлопной системе резко возрастает и уровень содержания кислорода в атмосферной камере зонда оказывается значительно ниже уровня содержания кислорода в отработавших газах, вследствие чего зонд генерирует напряжение 1V отрицательной полярности. Блок управления двигателем в таком случае считает лямбда-зонд исправным, так как вскоре после пуска двигателя и прогрева, датчик отклонил опорное напряжение и снизил его до ~0V.

Выходное напряжение зонда напряжением ~0V свидетельствует о близком уровне содержания кислорода в отработавших газах и в разгерметизированой атмосферной камере зонда. На блок управления двигателем поступает сигнал зонда низкого уровня, что является для него свидетельством обеднённой топливовоздушной смеси. Вследствие этого, блок управления двигателем обогащает топливовоздушную смесь. Таким образом, разгерметизация лямбда-зонда приводит к значительному обогащению топливовоздушной смеси. При этом многие системы самодиагностики выявить данную неисправность зонда не способны.
Широкополосный лямбда-зонд Выходной сигнал широкополосного лямбда-зонда в отличие от двухуровневых зондов несёт сведения не только о направлении отклонения состава рабочей смеси от стехиометрического, но и о его численном значении. Анализируя уровень выходного сигнала широкополосного лямбда-зонда, блок управления двигателем рассчитывает численное значение коэффициента отклонения состава рабочей смеси от стехиометрического состава, что, по сути, является коэффициентом лямбда.

Для широкополосных зондов производства BOSCH Выходное напряжение чувствительного элемента зонда (чёрный провод относительно жёлтого провода) изменяется в зависимости от уровня содержания кислорода в отработавших газах и от величины и полярности электрического тока, протекающего по кислородному насосу зонда (красный провод относительно жёлтого). Блок управления двигателем генерирует и подаёт на кислородный насос зонда электрический ток, величина и полярность которого обеспечивает поддержание выходного напряжения чувствительного элемента зонда на заданном уровне (450 mV). Если бы двигатель работал на топливовоздушной смеси стехиометрического состава, то блок управления двигателем установил бы на красном проводе напряжение равное напряжению на жёлтом проводе, и ток протекающий через красный провод и кислородный насос зонда был бы равен нулю.

При работе двигателя на обеднённой смеси, блок управления двигателем на красный провод подаёт положительное напряжение относительно жёлтого провода, и через кислородный насос начинает течь ток положительной полярности. При работе двигателя на обогащенной смеси, блок управления изменяет полярность напряжения на красном проводе относительно жёлтого провода, и направление тока кислородного насоса так же изменяется на отрицательное. Величина тока кислородного насоса устанавливаемая блоком управления двигателем зависит от величины отклонения состава топливовоздушной смеси от стехиометрического состава. В электрическую цепь кислородного насоса включен измерительный резистор, падение напряжения на котором и является мерой уровня содержания кислорода в отработавших газах.
Проблемы
Проблема заключается в следующем, цена на новый ЛЗ сейчас очень высока. На рынках в магазинах сейчас очень часто попадаются бракованные, поддельные ЛЗ, в случае установки его в выпуск, обратно вернуть его уже весьма проблематично.
Из того что испытывалось, нагрев строительным феном ЛЗ до 350 С с подачей опорного напряжения 0,45 в никакой реакции (способ найден в инете!) на ламповом оссцилоскопе с высоким входным сопротивлением.
Но порадовало одно у чуствительного элемента ЛЗ есть емкость где то в районе 50-80 Пикофарад.
Другой более надежный способ рожденный опытом это берем газовый паяльник и нагреваем чуствительный элемент при этом разьем лямды подключен к эбу и смотрим на отклонение напряжения от опорного, в небольших пределах мы увидим отклонение что косвенно потверждает его исправность.
Меня интересуют варианты безустановочной диагностики ЛЗ. Буду рад любым идеям, даже самым бредовым на первый взгляд.

Прим. редактора: очень интересная статья с GeekTimes про историю изучения т.н. космологической постоянной. Я позволил себе немного подкорректировать автора, но изложения стиль сохранил. Пусть не смущают вас в начале формулы - изложено человеческим языком, понятно и увлекательно.

Автор статьи: хабраюзер Vanxant

Что это вообще за космологическая постоянная?

Первую версию Общей Теории Относительности (ОТО) Альберт Эйнштейн представил публике 25 ноября 1915 года. В оригинале уравнения ОТО Эйнштейна выглядели вот так:

Прим. редактора: К дальнейшему изложению это отношения не имеет, но возможно кому-то будет интересно, здесь в фигурных скобках в формулах [2] и [3] записаны индексы символов Кристоффеля.

В современной записи это выглядит вот так:

Для неумеющего в тензоры читателя понятнее уравнение [1] в оригинальной записи Эйнштейна. Там написано, что энергия-импульс материи G равен кривизне пространства R плюс тензор Риччи S. В общем-то, этот самый тензор Риччи тоже есть кривизна, только в другой форме. Сейчас, решая уравнение ОТО, энергию-импульс обычно считают известным, а ищут как раз кривизну. Поэтому в современной записи стороны уравнения поменяли местами. Заодно поменяли буковки: G→T, S→R_μν.

Откуда есть пошла лямбда

Одним из первых серьёзных математиков, который занялся проверкой выкладок Эйнштейна, стал Эли Жозеф Картан (не путать с его сыном Анри, тоже известным математиком).

Но физика — это вам не математика. Здесь нельзя взять формулу и напихать в неё добавочных слагаемых просто так. Нужно иметь очень веские основания, и теоретические, и экспериментальные.

Хотя ниже вы увидите, насколько мало Эйнштейн знал о Вселенной в те годы, но тогда, в 1916, такие основания у него были. Альберт Германович точно знал, что звёзды не попадали друг на друга и совершенно не собираются этого делать в обозримом будущем. Однако, в ОТО-1915 было только притяжение, которое нужно было чем-то сбалансировать.

Первое физическое толкование смысла лямбды

В такой трактовке ненулевое значение Λ означает, что наша Вселенная искривлена сама по себе, в том числе и при отсутствии какой-либо гравитации. Ну, вот такой нам достался мир. Однако, большинство физиков в это не верят, и считают, что у наблюдаемого искривления должна быть какая-то внутренняя причина. Какая-то неведомая доселе фигня, которую можно открыть.

На сегодняшний день измеренная кривизна пространства Вселенной таки равна нулю, но с очень паршивой точностью, порядка 0.4%. И не очень-то видно способов эту точность улучшить. С измерениями кривизны есть две концептуальные проблемы.

Первая в том, что мы не можем измерить совсем пустое пространство, потому что просто ничего там не видим. А если там есть что-то, что мы таки видим, то пространство уже не пустое и, значит, уже дополнительно искривлено гравитацией.

Допустим, у нас есть как-то измеренные координаты объектов, плюс пачка фотографий этих объектов в разных ракурсах (снятых из разных точек). Тогда мы можем вычислить кривизну пространства. Например, гравитация Солнца отклоняет пролетающий мимо свет далёких звёзд. Во время солнечных затмений это отклонение можно измерить экспериментально и сравнить с предсказаниями ОТО.

Теперь наоборот: допустим, мы знаем кривизну пространства, и у нас есть пачка фотографий. Тогда, если кривизна достаточно хорошая, без чёрных дыр и т.п. — мы можем вычислить координаты объектов на фото. Именно так работают наши глаза, точнее мозги, когда вычисляют расстояние до объектов по двум фоткам с разных точек.

Поэтому измерить кривизну наблюдаемой Вселенной в целом мы можем только из очень окольных соображений.

Вселенная Фридмана

Meanwhile in Russia, не смотря на войны и революции, над теорией ОТО бился прапорщик (и по совместительству профессор) Александр Александрович Фридман. Он рассмотрел все варианты лямбд и выяснил следующее:

Но самое интересное происходит при Λ = 0. Здесь всё зависит от начальных условий — т.е. координат и скоростей конкретных галактик. Возможны три варианта: большое сжатие, большой разлёт и стационарный вариант, когда галактики разлетаются, но с относительно небольшими скоростями и без ускорения.

Сегодня вышеописанные ситуации называются космологическими решениями Фридмана.

Статьи Фридмана 1922 и 1924 годов отменяли необходимость в лямбда-члене, из-за чего поначалу были приняты Эйнштейном в штыки.

За свою работу Фридман вполне мог претендовать на Нобелевку.

Летом 1925 он женился, поехал в свадебное путешествие в Крым, съел там немытую грушу, заразился тифом и в сентябре — умер.

Возвращаясь к расширению вселенной, можно привести примерно такой график (конкретно на этом учтены данные на 2010 год):

Здесь по горизонтали отложено z — это красное смещение, по вертикали наблюдаемая яркость сверхновых особого типа Ia, которые всегда выделяют одно и то же количество энергии. Вообще, это два способа измерения одного и того же расстояния, но, так сказать, в разные моменты времени.

Серые палки — наблюдавшиеся события с их погрешностью измерений. Синим пунктиром отложено предсказание при Λ = 0, красной линией — аппроксимация фактически наблюдаемых значений. Отклонение красной линии от прямой означает, что Вселенная расширяется ускоренно. Но Эйнштейн об этом так и не узнал.

Вселенная Каптейна

Перейдём к экспериментальной части. Голландский астроном Якобус Корнелиус Каптейн открыл звезду Каптейна в 1897, после чего приступил к opus magnum всей своей жизни. Объединяя огромное количество наблюдений разных обсерваторий, он попытался создать первую карту Вселенной. По его карте выходило, что вселенная имеет форму вращающегося (sic!) диска крышесносящего по тем временам размера 40000 световых лет, причём Солнце находится отнюдь не в центре, а вполне себе на задворках. Закончена и опубликована эта работа была только в 1922.

Для понимания уровня тогдашних знаний: то, что Каптейн считал невероятно огромной Вселенной, сегодня считается совершенно рядовой, ничем не примечательной среди миллиардов таких же… галактикой Млечный Путь. Тем не менее, заслуга Каптейна в том, что он открыл её вращение и приблизительно вычислил её центр.

Наблюдения Хаббла (астронома, а не телескопа)

Статью со своими открытиями, из которой следовало, что Вселенная значительно больше, чем наш Млечный путь, Хаббл представил американскому астрономическому обществу первого января 1925. За что и был освистан страдающими от похмелья коллегами, едва свыкшимися с расстояниями Каптейна.

Хаббл не унимался и прикрутил к телескопу ещё и спектрометр. Анализируя красное смещение галактик, он выяснил, что галактики разбегаются, а Вселенная, соответственно, расширяется. Заодно он открыл закон имени себя с константой имени себя (впрочем, закон был предсказан Леметром), и описал всё это в статьях к концу 20-ых годов. Согласно его наблюдениям, оказалась верна модель Фридмана для Λ = 0.

Это выбило из-под лямбды теперь уже и экспериментальные основания её существования.

Здесь ещё нужно упомянуть, что первоначальные оценки Хаббла были очень уж неточными и показывали возраст Вселенной порядка 2 миллиардов лет. Позднее это войдёт в противоречие с данными геофизиков, которые при помощи радиоизотопного анализа оценят возраст Земли в несколько миллиардов лет, и десятилетиями будет сильнейшей головной болью для физиков-космологов.

Стационарная Вселенная Хойла

С начала 30-ых годов вопрос с лямбдой считался решённым, и из мейнстримных физиков ей никто толком не занимался. Одним из редких исключений, рискнувших попереть супротив самого Эйнштейна, стал британец Фред Хойл.

Речь пойдёт о гелии. Этот элемент феноменально инертен и не хочет ни с чем реагировать. Причём не только химически, но и физически тоже, если мы говорим про гелий-4. Его ядро — альфа частица — имеет пиковую энергию связи на нуклон в своей области. см. рис из какого-то реферата:

Это значит, что альфа-частица не может присоединить дополнительные протоны или другую альфа-частицу иначе как случайно: это просто-напросто энергетически невыгодно. А в ядрах звёзд ничего кроме протонов и альфа-частиц и нет.

Возникал резонный вопрос: а откуда, собственно, взялись химические элементы тяжелее гелия?

Ближайшее ядро, в которое может превращаться гелий-4, это углерод-12. Но для этого нужно объединить три альфа-частицы.

Проблема в том, что вероятность столкновения трёх альфа-частиц одновременно слишком мала. А двухшаговый процесс (сначала сталкиваются две частицы, потом очень быстро, пока они не разлетелись обратно на две альфа-частицы, в них врезается ещё одна), в принципе, возможен, но расчёты Эдвина Солпитера показывали, что такой процесс идёт слишком вяло, чтобы производить существенные количества углерода.

Однако, по расчётам Хойла выходило, что при наличии такого уровня в три-альфа процессе наступает резонанс, и звёзды — красные гиганты производят достаточно много углерода для нашего существования.

Удивительно, но американцы решили провести небольшой эксперимент на своём ускорителе. И да — триумфально нашли нужный энергетический уровень на 7.65 МэВ, который физики-ядерщики всего мира почему-то проглядели во всех предыдущих экспериментах.

Сегодня такое возбуждённое состояние углерода-12, когда три альфа-частицы фактически выстраиваются по линии, называется хойловским. Соответствующая статья Хойла, Фаулера и супругов-астрономов Джефри и Маргерит Бёрбиджей является краеугольным камнем современных теорий звёздного нуклеосинтеза и настолько часто цитируется, что обозначается просто B 2 FH, без ссылок и расшифровок.

И — да, на сегодня это чуть ли не единственное известное успешное предсказание на основе антропного принципа.

Однако, из квантовых флуктуаций постоянно рождается новое вещество, причём так, что средняя плотность материи остаётся одинаковой. Расчёты показывают, что в одном кубическом километре пространства должен рождаться всего-навсего один протон раз в 300000 лет (а так же один электрон или что-то типа того для сохранения электрического заряда). Прекрасное число, чтобы исключить любую возможность какой-либо экспериментальной проверки!

Теория стационарной Вселенной серьёзно рассматривалась как альтернатива теории Большого Взрыва в 50-х и начале 60-х. Но экспериментальное открытие в 1964 году предсказанного ТББ реликтового излучения поставило на ней крест.

За статью B 2 FH дали Нобелевку. Но только Фаулеру, который распорядился провести десятидневный эксперимент. Ни супругам Бёрбиджам, проводившим длительные астрономические наблюдения и собственно написавшим статью, ни автору идеи Хойлу нобелевку не дали — за упорствование в космологической ереси.

Квантовая лямбда

Вернёмся к уравнению ОТО. Слева (в современной записи) стоит кривизна пространства, сиречь гравитация по ОТО. Справа — тензор энергии-импульса. Под этим тензором стоит жутко сложный матан, но суть в следующем: там учтена вся-вся-вся материя Вселенной во всех видах и состояниях. И обычное вещество, и всякие хитрые частицы, и все виды излучений (кроме гравитации, которая слева).

Теперь мысленно перенесём лямбду вправо. В такой записи это будет не дополнительная кривизна, а какая-то неучтённая энергия (замечу, отрицательная, раз уж мы считаем лямбду положительной). И здесь просматриваются две возможности.

Первая гипотеза состоит в том, что лямбда — это энергия собственно вакуума. Звучит диковато, но на самом деле вполне согласуется с квантовой механикой. Возьмём кусок пространства и уберём из него всё, что хотя бы в принципе можно убрать. Уберём всё вещество, все частицы и все волны, независимо от их природы. Останутся только физические поля в невозмущённом состоянии. Полный штиль.

Так вот, у некоторых полей (например, Хиггсовских) в пустоте ненулевое значение. И теоретически у них есть некоторая энергия. Кроме того, в силу принципа неопределённости у любых полей есть квантовые флуктуации — и они тоже имеют некоторую энергию.

Вместо заключения

Звоночки о ненулевом значении лямбды начали появляться на рубеже 90-ых — из точных измерений реликтового излучения (там обнаружили когерентность реликтового излучения на слишком больших масштабах. Могло просто случайно так совпасть, мог быть какой-то неучтённый эффект, но более вероятной была гипотеза с расширением) и т.д., и к 1997 звоночки превратились в набат.

Читайте также: