Оценка лямбда параметра распределения лямбда называется несмещенной если

Обновлено: 05.07.2024

или ожидаемым значением [см. II, раздел 10.4.1]. По соображениям простоты обычно выбирают ожидаемое значение. И вновь требование близости выборочного математического ожидания к в недостаточно определенно. В конце концов потребуем совпадения в и математического ожидания в. Оценка в в таком случае называется несмещенной. Разброс выборочного распределения удобно измерять дисперсией. Итак, мы подошли к несмещенным оценкам с минимальной дисперсией.

Определение 3.3.2. Несмещенная оценка. Пусть — оценка в, основанная на данных, в которых — реализации случайной величины Она называется несмещенной оценкой , если при всех

Оценка, которая не является несмещенной, называется смещенной. Смещение определяется соотношением

Несмещенная оценка с минимальной дисперсией может подчиняться дополнительным требованиям к форме ее функциональной зависимости от (таким, как линейность и т. п.).

Из этого следует, что свойство несмещенности не принадлежит к важнейшим в первую очередь из-за неинвариантности при функциональных заменах (кроме линейных). Предположим, что мы интересуемся некоторым технологическим процессом и оцениваем вероятность того, что X не превышает заданной величины т. е. мы хотим оценивать значение , где — функция распределения X. Если в — несмещенная оценка , то в общем случае не будет несмещенной для . Для подобных приложений, следовательно, несмещенность является бесполезной.

С тем же сталкиваемся и в следующей ситуации. Если в испытаниях Бернулли с вероятностью успеха в зафиксировано успехов, то оценка — несмещенная для однако смещено относительно

Наконец, несмещенные оценки — не обязательно более точные, чем смещенные. Известный пример — несмещенная оценка дисперсии генеральной совокупности. Средняя квадратичная ошибка смещенной оценки меньше, чем

Почему же тогда несмещенность приобрела такое важное значение для статистических правил? Причины — в математических удобствах, в линейности и состоятельности: оператор математического ожидания имеет много свойств, облегчающих работу с ним; многие важные статистики являются линейными функциями наблюдений, а несмещенность инвариантна относительно линейных преобразований; независимые несмещенные оценки можно комбинировать и получать более точные несмещенные оценки.

Построение несмещенных оценок с минимальной дисперсией НОМД обычно связывают с понятием достаточности. Дополнительные сведения по этому поводу содержатся в разделе 3.4.

Следующие примеры относятся к минимизации дисперсии в определенных классах оценок (линейных, квадратичных и т. д.).

Пример 3.3.4. Линейная несмещенная оценка с минимальной дисперсией (ЛНОМД). Пусть — случайная выборка наблюдений за переменной X, для которой и Чтобы найти ЛНОМД для , составим линейную функцию от наблюдений, скажем

Выборочное математическое ожидание [см. раздел 2.3] равно

Чтобы оно в точности было равно , т. е. необходимо положить

Последний шаг состоит в выборе минимизирующем выборочную дисперсию Легко видеть, что при условии достигает своего минимального значения, когда (Минимизация обсуждается в [IV, раздел 15.1.3].) Итак, является ЛНОМД для . Общая теория ЛНОМД будет детально исследована при обсуждении метода наименьших квадратов в гл. 8, 10.

Пример 3.3.5. Квадратичная несмещенная оценка с минимальной дисперсией (КНОМД). Дисперсия случайной переменной X имеет размерность В соответствии с принципом правильной размерности [см. раздел 3.3.1, а)] мы требуем, чтобы оценка тоже имела размерность . Простейшая такая функция — квадратичная форма [см. I, гл. 9] от значений выборки скажем

где транспонирование и — симметрическая -матрица [см. I, раздел 6.2]. Согласно принципу заменяемости [см. раздел 3.3.1, б)] должна иметь вид

Выборочное математическое ожидание, следовательно, будет равно [см. II, раздел 9.2.1]:

По свойству несмещенности оно должно быть равно откуда (кроме тех случаев, когда в — заведомый нуль)

Следовательно, определяются однозначно принципами заменяемости и несмещенности. В этом частном случае применение принципа заменяемости фактически эквивалентно минимизации выборочной дисперсии [см. теорему 3.3.1]. Из этого следует, что КНОМД есть

Преобразив это выражение, мы придем к уже известной нам оценке

Пример 3.3.6 (продолжение). В особо простом случае, когда принцип заменяемости применяется так же, а условие несмещенности становится проще: Мы, следовательно, получаем оценку

где пока не определено. Вычисления показывают, что выборочная дисперсия этой статистики равна Это выражение обращается в минимум при Таким образом, в данном случае КНОМД равна ее выборочная дисперсия —

Следующая теорема Халмоша связывает понятие несмещенной оценки с минимальной дисперсией и принцип заменяемости [см. раздел 3.2.1, б)].

Теорема 3.3.1. Симметричные оценки. Пусть — выборка взаимозаменяемых наблюдений X и — несмещенная оценка в параметра распределения X. Если — несимметрическая функция х, определим симметризацию как , где для каждого есть (вне зависимости от порядка нумерации) из перестановок [см. I, раздел 8.1] множества из элементов Мы примем за тождественную перестановку, т. е. Тогда несмещенная оценка , а выборочная дисперсия меньше, чем у статистики Если симметрическая функция, то совпадает с

Это означает, например, что среди всех линейных несмещенных оценок математического ожидания в среднее по выборке будет наилучшей, т. е. будут иметь наименьшую дисперсию. (Общий вид линейной

оценки с произвольными коэффициентами Выборочное математическое ожидание ее равно и для того, чтобы это выражение было равным 0, чего требует несмещенность, должно быть Следовательно, несмещенная линейная оценка 0 есть Ее симметризация имеет вид и согласно теореме Халмоша она имеет меньшую дисперсию, чем любая другая несмещенная линейная оценка пример

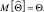
Предположим, что мы производим оценку неизвестного неслучайного параметра Θ и в результате измерений получаем так называемую несмещенную оценку, т.е. такую оценку, математическое ожидание которой равняется значению самого оцениваемого параметра, т.е. Для того чтобы определить качество оценки, следует определить ее дисперсию, которая вычисляется следующим образом:

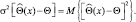
Дисперсия дает меру рассеяния ошибки. Наилучшей оценкой была бы, по-видимому, несмещенная оценка с минимальной дисперсией. Однако регулярной процедуры, которая бы приводила к получению алгоритма, формирующего несмещенную оценку с минимально возможной дисперсией, не существует.

В этой ситуации имеет смысл получить выражение для нижней границы дисперсии любой несмещенной оценки. Знание границы позволит сравнить дисперсию той или иной оценки с этой границей, и в том случае, если будет получено совпадение дисперсии оценки с нижней границей, может быть сделан вывод, что мы получили наилучшую оценку. Если же точное совпадение не обеспечено, то и в этом случае мы можем судить, насколько наша оценка отличается от потенциально достижимой.

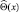
Докажем следующее утверждение. Если – любая несмещенная оценка величины Θ, то

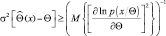
(2.9.1)

или, что эквивалентно,

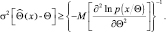
(2.9.2)

При этом мы считаем, что производные

существуют и являются абсолютно интегрируемы.

Неравенства (2.9.1) и (2.9.2) обычно называются границами Крамера-Рао. Любая оценка, удовлетворяющая указанной границе со знаком равенства, называется эффективной оценкой.

Доказательство этого положения основано на использовании неравенства Буняковского-Шварца. Так как по нашему предположению оценка считается несмещенной, запишем

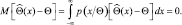
(2.9.3)

Дифференцируя обе части по Θ, имеем

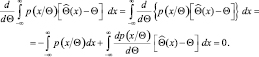
(2.9.4)

Первый интеграл равен 1. Кроме того, заметим, что

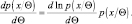
(2.9.5)

Подставляя (2.9.5) в (2.9.4), получаем

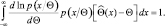
Перепишем подынтегральное выражение в следующем виде:

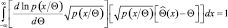
и используем неравенство Буняковского-Шварца:

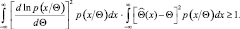
(2.9.6)

В связи с тем, что каждый из сомножителей представляет собой математическое ожидание, имеем следующее неравенство:

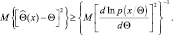
Итак, неравенство (2.9.1) можно считать доказанным. Для доказательства неравенства (2.9.2) заметим, что

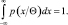
Дифференцируя по Θ, имеем

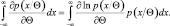
(2.9.7)

Вновь дифференцируя по Θ и применяя (2.9.5), получим

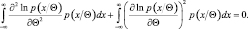
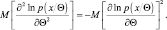
Последнее равенство означает справедливость условия (2.9.2).

Неравенство Крамера-Рао позволяет сделать ряд важных замечаний.

1. Любая несмещенная оценка имеет дисперсию больше, чем некоторое число.

2. Неравенство Буняковского-Шварца (2.9.6) выполняется тогда и только тогда, когда

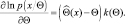
(2.9.8)

Если эффективная оценка существует (равенство (2.9.8) выполняется), то эта оценка является оценкой максимального правдоподобия. Действительно, уравнение правдоподобия имеет вид

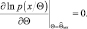
Для того чтобы правая часть равенства (2.9.8) принимала нулевое значение, оценка должна быть равна .

3. Если эффективной оценки не существует (равенство (2.9.8) не выполняется), то неизвестно, насколько оптимальной является оценка максимального правдоподобия (насколько близко она приближается к границе). В этой ситуации границу и дисперсию оценки приходится вычислять и полученные величины сравнивать. Однако достаточно обнадеживающим является тот факт, что оценка по максимуму правдоподобия является асимптотически эффективной, иначе говоря, при стремлении размера выборки (размерности вектора x к бесконечности) дисперсия оценки максимального правдоподобия стремится к своей границе.

Несмещённая оце́нка в математической статистике — это точечная оценка, математическое ожидание которой равно оцениваемому параметру.

Определение

Пусть — выборка из распределения, зависящего от параметра . Тогда оценка называется несмещённой, если

В противном случае оценка называется смещённой, и случайная величина называется её смеще́нием.

Примеры

— исправленная выборочная дисперсия.

Литература и некоторые ссылки

Полезное

Несмещенная оценка — (unbiased estimator) статистическая точечная оценка, математическое ожидание которой совпадает с оцениваемой величиной (у нее нет систематической ошибки) … Экономико-математический словарь

НЕСМЕЩЕННАЯ ОЦЕНКА — (unbiased estimator) Статистический показатель, не слишком отличающийся от среднего значения. Метод оценки не всегда дает показатели, соответствующие реальности, но отклонения в любую сторону равновероятны. Экономика. Толковый словарь. М.: ИНФРА… … Экономический словарь

несмещенная оценка — 2.55. несмещенная оценка Оценка со смещением, равным нулю Источник: ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения … Словарь-справочник терминов нормативно-технической документации

несмещенная оценка — nepaslinktasis įvertis statusas T sritis Standartizacija ir metrologija apibrėžtis Įvertis, kurio poslinkis lygus nuliui. atitikmenys: angl. unbiased estimator rus. несмещенная оценка, f pranc. estimateur sans biais, m … Penkiakalbis aiškinamasis metrologijos terminų žodynas

несмещенная оценка — Оценка параметра называется несмещенной, если ее ожидаемое значение (математическое ожидание) равняется истинному значению параметра. В противном случае оценка является смещенной … Словарь социологической статистики

ОЦЕНКА СТАТИСТИЧЕСКАЯ — функция от случайных величин, применяемая для оценки неизвестных параметров теоретич. распределения вероятностей. Методы теории О. с. служат основой современной теории ошибок; обычно в качестве неизвестных параметров выступают измеряемые физич.… … Математическая энциклопедия

ОЦЕНКА НАИЛУЧШАЯ ЛИНЕЙНАЯ НЕСМЕЩЕННАЯ — (Best linear unbiased estimation). Результат решения смешанной модели, относящейся к фиксированным факторам. Процедура наилучшей линейной несмещенной оценки используется в случаях, когда требуется оценить (а не спрогнозировать) влияние каких либо … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных

Статистическое оценивание

Материал из MachineLearning.

Содержание

Постановка задачи

Различают два основных типа оценок: точечные оценки и доверительные интервалы.

Точечное оценивание

К общим методам построения точечных оценок параметров относятся: метод максимального правдоподобия, метод моментов, метод квантилей.

Ниже приводятся некоторые свойства, которыми могут обладать или не обладать точечные оценки.

Состоятельность

Когда употребляют просто термин состоятельность, то обычно имеется в виду слабая состоятельность, т.е. сходимость по вероятности.

Условие состоятельности является практически обязательным для всех используемых на практике оценок. Несостоятельные оценки используются крайне редко.

Несмещенность и асимптотическая несмещенность

Оценка параметра называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра:

Более слабым условием является асимптотическая несмещенность, которая означает, что математическое ожидание оценки сходится к истинному значению параметра с ростом объема выборки:

Сравнение оценок и эффективность

Для сравнения между собой различных оценок одного и того же параметра применяют следующий метод: выбирают некоторую функцию риска, которая измеряет отклонение оценки от истинного значения параметра, и лучшей считают ту, для которой эта функция принимает меньшее значение.

Чаще всего в качестве функции риска рассматривают математическое ожидание квадрата отклонения оценки от истинного значения

Существует нижняя граница на данную функцию риска, называемая неравенство Крамера-Рао.

(Несмещенные) оценки, для которых достигается эта нижняя граница (т.е. имеющие минимально возможную дисперсию), называются эффективными. Однако существование эффективной оценки есть довольно сильное требование на задачу, которое имеет место далеко не всегда.

Достаточные статистики

(Несмещенная) эффективная оценка параметра всегда является достаточной статистикой.

Доверительные интервалы

Другим типом оценок статистических параметров являются доверительные интервалы.

Доверительные интервалы используются, когда нам нужны надежные границы, в которые попадает значение оцениваемого параметра.

Часто вместе с точечной оценкой параметра строят доверительный интервал, середина которого равна этой оценке. Его ширина является наглядной характеристикой того, насколько точна может быть данная точечная оценка.

Иногда бывает наоборот: естественным образом строится некоторый доверительный интервал, а в качестве точечной оценки параметра рассматривают его середину.

Статистическое оценивание

Материал из MachineLearning.

Содержание

Постановка задачи

Различают два основных типа оценок: точечные оценки и доверительные интервалы.

Точечное оценивание

Ниже приводятся некоторые свойства, которыми могут обладать или не обладать точечные оценки.

Состоятельность

Несмещенность и асимптотическая несмещенность

Сравнение оценок и эффективность

Существует нижняя граница на данную функцию риска, называемая неравенство Крамера-Рао.

Достаточные статистики

(Несмещенная) эффективная оценка параметра всегда является достаточной статистикой.

Доверительные интервалы

Другим типом оценок статистических параметров являются доверительные интервалы.

Несмещённая оценка

Определение

Пусть — выборка из распределения, зависящего от параметра . Тогда оценка называется несмещённой, если

В противном случае оценка называется смещённой, и случайная величина называется её смеще́нием.

Примеры

— исправленная выборочная дисперсия.

Тогда является смещённой, а несмещённой оценками параметра . Смещенность можно доказать следующим образом:

Где и — среднее и его оценка соответственно.

Литература и некоторые ссылки

Полезное

Несмещённая оценка — оценка параметра Распределения вероятностей по наблюдённым значениям, лишённая систематической ошибки. Более точно: если оцениваемое распределение зависит от параметров θ1, θ2. θs, то функция θi* (x1, x2. xn) от результатов… … Большая советская энциклопедия

Состоятельная оценка — статистическая оценка параметра Распределения вероятностей, обладающая тем свойством, что при увеличении числа наблюдений вероятность отклонений оценки от оцениваемого параметра на величину, превосходящую некоторое заданное число,… … Большая советская энциклопедия

СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ — один из осн. разделов матем. статистики … Физическая энциклопедия

Статистические оценки — функции от результатов наблюдений, употребляемые для статистического оценивания (См. Статистическое оценивание) неизвестных параметров распределения вероятностей изучаемых случайных величин. Например, если X1. Xn независимые случайные … Большая советская энциклопедия

Неравенство Крамера — Рао — В математической статистике неравенством Крамера Рао (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая… … Википедия

Неравенство Крамера — В математической статистике неравенством Крамера Рао (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая… … Википедия

Статистика (функция выборки) — У этого термина существуют и другие значения, см. Статистика (значения). Статистика (в узком смысле) это измеримая числовая функция от выборки, не зависящая от неизвестных параметров распределения. В широком смысле термин (математическая)… … Википедия

Несмещённая оценка

Полезное

СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ — один из осн. разделов матем. статистики … Физическая энциклопедия

Пусть Х – количественный признак элементов генеральной совокупности. Вид закона распределения этого признака известен (например, признак Х распределен нормально), но не известны параметры закона. Требуется оценить (установить) эти параметры по выборке, извлеченной из генеральной совокупности.

Оценки неизвестного параметра Ө могут быть точечными и интервальными.

Точечная оценка определяется одним числом, а интервальная – интервалом, который с заранее заданной вероятностью (надежностью) покрывает неизвестный параметр.

Пусть значение оцениваемого параметра Ө, определенное по выборке, равно Ө*.

Точечная оценка называется:

несмещенной, если математическое ожидание Ө* равно Ө, т. е. М(Ө *) = Ө;
смещенной – в противном случае: М(Ө*) ≠ Ө.

Несмещенная оценка, имеющая минимальную дисперсию, называется эффективной .

Несмещенная оценка, дисперсия которой стремится к нулю при n ∞ (n – объем выборки), называется состоятельной .

Точечные оценки математического ожидания и дисперсии

Несмещенной оценкой генеральной средней является выборочная средняя . Она определяется по формуле:

где x_i - i-ое значение варианты; n_i - соответствующая частота; n - объем выборки.

Несмещенной оценкой генеральной дисперсии является

Последнее выражение называется исправленной дисперсией.

Метод максимума правдоподобия оценивания параметров распределения

В этом методе в качестве оценки неизвестного параметра выбирается такая, при которой вероятность полученной выборки становится наибольшей.

Пусть p(x, Θ) - плотность вероятности случайной величины, зависящая от параметра Θ. Для нахождения оценки неизвестной величины Θ проведены опыты (измерения); получены значения x₁, x₂, …, x_n.

Функцией правдоподобия называется функция

В методе максимума правдоподобия в качестве оценки величины Θ выбирается значение, при котором функция L(Θ) имеет максимум. Для этого нужно решить уравнение

или равносильное ему, но обычно более простое, уравнение правдоподобия :

Читайте также: