Выберите верный вариант проверки устойчивости стержня гибкость стержня лямбда 25
Обновлено: 30.06.2024
Пример 1. Рассчитать гибкость стержня. Круглый стержень диаметром 20 мм закреплен так, как показано на рис. 37.1.

Решение
1. Гибкость стержня определяется по формуле


2. Определяем минимальный радиус инерции для круга.
Подставив выражения для Jmin и А (сечение круг)


- Коэффициент приведения длины для данной схемы крепления μ= 0,5.
- Гибкость стержня будет равна

Пример 2. Как изменится критическая сила для стержня, если изменить способ закрепления концов? Сравнить представленные схемы (рис. 37.2)
Решение


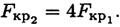
Критическая сила увеличится в 4 раза.

Пример 3. Как изменится критическая сила при расчете на устойчивость, если стержень двутаврового сечения (рис. 37.3а, двутавр № 12) заменить стержнем прямоугольного сечения той же площади (рис. 37.3б)? Остальные параметры конструкции не меняются. Расчет выполнить по формуле Эйлера.
Решение
1. Определим ширину сечения прямоугольника, высота сечения равна высоте сечения двутавра. Геометрические параметры двутавра № 12 по ГОСТ 8239-89 следующие:
площадь сечения А1 = 14,7см 2 ;

минимальный из осевых моментов инерции .
По условию площадь прямоугольного сечения равна площади сечения двутавра. Определяем ширину полосы при высоте 12 см.

2. Определим минимальный из осевых моментов инерции.

3. Критическая сила определяется по формуле Эйлера:
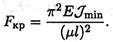
4. При прочих равных условиях отношение критических сил равно отношению минимальных моментов инерции:

5. Таким образом, устойчивость стержня с сечением двутавр № 12 в 15 раз выше, чем устойчивость стержня выбранного прямоугольного сечения.

Пример 4. Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение — швеллер № 16, материал — СтЗ, запас устойчивости трехкратный. Стержень нагружен сжимающей силой 82 кН (рис. 37.4).
Решение
1. Определяем основные геометрические параметры сечения стержня по ГОСТ 8240-89. Швеллер № 16: площадь сечения 18,1см 2 ; минимальный осевой момент сечения 63,3 см 4 ; минимальный радиус инерции сечения гт;п = 1,87см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала СтЗ λпред = 100.
Расчетная гибкость стержня при длине l = 1м = 1000мм

Рассчитываемый стержень — стержень большой гибкости, расчет ведем по формуле Эйлера.

3. Допускаемая нагрузка на стержень


4. Условие устойчивости

82кН 5 и σпц = 450 Н/мм 2 .

Решение
Для расчёта на устойчивость должна быть известна критическая сила для заданной стойки. Необходимо установить, по какой формуле следует вычислять критическую силу, т. е. надо сопоставить гибкость стойки с предельной гибкостью для её материала.
Вычисляем величину предельной гибкости, так как табличных данных о λ,пред для материала стойки не имеется:

Для определения гибкости рассчитываемой стойки вычисляем геометрические характеристики ее поперечного сечения:

Определяем гибкость стойки:

и убеждаемся, что λ [nу] на 5,2%.
Пример 2.87. Проверить на прочность и устойчивость заданную стержневую систему (рис. 2.86), Материал стержней — сталь Ст5 (σт = 280 Н/мм 2 ). Требуемые коэффициенты запаса: прочности [n] = 1,8; устойчивости [nу] = 2,2. Стержни имеют круглое поперечное сечение d1 = d2 = 20 мм, d3 = 28 мм.
Решение

Вырезая узел, в котором сходятся стержни, и составляя уравнения равновесия для действующих на него сил (рис. 2.86)

устанавливаем, что заданная система статически неопределима (три неизвестных усилия и два уравнения статики). Ясно, что для расчета стержней на прочность и устойчивость необходимо знать величины продольных сил, возникающих в их поперечных сечениях, т. е. нужно раскрыть статическую неопределимость.
Составляем уравнение перемещений на основе диаграммы перемещений (рис. 2.87):

или, подставляя значения изменений длин стержней, получаем


Решив это уравнение совместно с уравнениями статики, найдем:

Напряжения в поперечных сечениях стержней 1 и 2 (см. рис. 2.86):

Их коэффициент запаса прочности

Для определения коэффициента запаса устойчивости стержня 3 надо вычислить критическую силу, а это требует определения гибкости стержня, чтобы решить, какой формулой для нахождения NKp следует воспользоваться.


Коэффициент запаса устойчивости
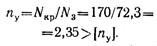
Таким образом, расчет показывает, что коэффициент запаса устойчивости близок к требуемому, а коэффициент запаса прочности значительно выше требуемого, т. е. при увеличении нагрузки системы потеря устойчивости стержнем 3 вероятнее, чем возникновение текучести в стержнях 1 и 2.
В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых один или два размера поперечного сечения малы по сравнению с длиной стержня. Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней: при достижении сжимающей силой F некоторой критической величины, равной Fкр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении Fкр стержень начинает интенсильно искривляется (выпучивается). При этом новым (моментным) равновесным состоянием упругого длинного становится некоторая новая уже криволинейная форма. Это явление носит название потери устойчивости.
Рис. 37. Потеря устойчивости
Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях.
Критическая сила (Fкр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела. Условие устойчивости:
Устойчивость сжатого стержня. Задача Эйлера.
При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил Л. Эйлер в 1744 году.
Рис. 38. Сжатый стержень
Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F. Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M:
где y – прогиб стержня в произвольном сечении с координатой x.
Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:

(26)
Проведя преобразования, можно увидеть, что минимальное значение критическая сила примет при n = 1 (на длине стержня укладывается одна полуволна синусоиды) и J = Jmin (стержень искривляется относительно оси с наименьшим моментом инерции)

(27)
Это выражение – формула Эйлера.
Зависимость критической силы от условий закрепления стержня.
Формула Эйлера была получена для, так называемого, основного случая – в предположении шарнирного опирания стержня по концам. На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды.
Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.



Рис. 39. Различные случаи закрепления стержня
Общая формула Эйлера:

(28)
где μ·l = lпр – приведенная длина стержня; l – фактическая длина стержня; μ – коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки. (Другая интерпретация коэффициента приведенной длины: μ показывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)
Таким образом, окончательно условие устойчивости примет вид

(29)
Рассмотрим два вида расчета на устойчивость сжатых стержней – проверочный и проектировочный.
Проверочный расчет
Порядок проверочного расчета на устойчивость выглядит так:
– исходя из известных размеров и формы поперечного сечения и условий закрепления стержня, вычисляем гибкость;
– по справочной таблице находим коэффициент понижения допускаемого напряжения, затем определяем допускаемое напряжение на устойчивость;
– сравниваем максимальное напряжение с допускаемым напряжением на устойчивость.
Проектировочный расчет
При проектировочном расчете (подобрать сечение под заданную нагрузку) в расчетной формуле имеются две неизвестные величины – искомая площадь поперечного сечения A и неизвестный коэффициент φ (так как φ зависит от гибкости стержня, а значит и от неизвестной площади A). Поэтому при подборе сечения обычно приходится пользоваться методом последовательных приближений:
– обычно в первой попытке принимают φ1 = 0,5…0,6 и определяют площадь сечения в первом приближении

– по найденной площади A1 подбирают сечение и вычисляют гибкость стержня в первом приближении λ1. Зная λ, находят новое значение φ′1;
– далее, используя найденный φ′1, проверяют условие устойчивости, и если σmaxmax и [σу] значительно отличаются друг от друга (более чем на 5 %), следует повторить расчет, приняв во второй попытке

Выбор материала и рациональной формы сечения.
Выбор материала. Так как в формулу Эйлера из всех механических характеристик входит лишь модуль Юнга, то для повышения устойчивости стержней большой гибкости нецелесообразно применять высокопрочные материалы, так как модуль Юнга для всех марок сталей примерно одинаков.
Для стержней малой гибкости применение высокосортных сталей оправдано, так как с повышением предела текучести у таких сталей повышаются и критические напряжения, а значит и запас устойчивости.
Форма сечения. При проектировании стержней, работающих на устойчивость, следует выбирать такую форму сечения, чтобы гибкость стержня была одинаковой относительно обеих главных осей его сечения (условие равноустойчивости), а значит максимальный и минимальный моменты инерции такого сечения должны быть одинаковы Jmax = Jmin.
Кроме того, необходимо стремиться к получению при данной площади наибольших радиусов инерции. Для этого необходимо выбирать сечения, большая часть площади которых по возможности была удалена от центра тяжести (трубчатые, коробчатые сечения).
По степени рациональности известные сечения можно распределить следующим образом: трубчатое сечение, коробчатое, двутавровое, состоящее из швеллеров, квадратное, круглое, прямоугольное.
Читайте также:

