Метод фурье лямбда появляется

Обновлено: 05.07.2024

Одномерный случай (одна пространственная переменная). Известно, что если функция удовлетворяет определенным условиям, то справедлива интегральная формула Фурье

Назовем образом Фурье функции функцию

в силу интегральной формулы Фурье функция может быть восстановлена с помощью формулы

Переход от называется интегральным преобразованием Фурье, а переход от называется обратным преобразованием Фурье.

Если же функция задана на полупрямой то можно рассматривать косинус-образ Фурье

переход от которого к оригиналу осуществляется по формуле

и синус-образ Фурье

переход от которого к оригиналу осуществляется по формуле

Основными свойствами преобразования Фурье являются:

1) линейность, т.е. произвольные постоянные);

2) преобразование частных производных, т. е. если и преобразование Фурье проводится по переменной то

(это доказывается интегрированием по частям), а образы частных производных по даются формулами

Таблица 2.1. Преобразование Фурье некоторых функций

Рис. 2.9. Блок-схема преобразования Фурье

(в предположении, что указанные частные производные по удовлетворяют определенным условиям).

Мы видим, что под действием преобразования Фурье операция дифференцирования по заменяется умножением. Этот важный факт используется при решении граничных задач для дифференциальных уравнений с частными производными.

Есть много других интересных свойств преобразований Фурье, на которых мы не останавливаемся. Примеры преобразования Фурье см. в табл. 2.1.

Вернемся к решению граничных задач для одномерного волнового уравнения. Чтобы решить такую задачу для переходят по переменной с помощью преобразования Фурье к задаче для образа Решив эту, более простую задачу, находят функцию с помощью обратного преобразования Фурье (рис. 2.9).

Пример 1 [4, гл. II, № 178]. Решить краевую задачу

Решение. Применим косинус-преобразование Фурье по переменной Пусть

Сразу проверим выполнение граничного условия Имеем

Дифференцирование по дает

откуда следует, что Тогда, учитывая, что

приходим к задаче Коши для обыкновенного дифференциального уравнения второго порядка

для определения функции Решение этой задачи имеет вид

Искомую функцию находим с помощью обратного косинус-преобразования Фурье:

Рассмотрим два случая.

Поскольку функция определена только для положительных значений то нужно преобразовать последний интеграл:

Итак, искомое решение есть

Замечание 1. В качестве функций могут быть, например, взяты функции и т.д.

Замечание 2. Для решения задач на полуограниченной прямой с граничным условием нужно воспользоваться синус-преобразованием Фурье, так как, если

Рассмотрим более сложную задачу на применение преобразования Фурье.

Пример 2 [4, гл. II, № 176]. Решить задачу Коши

Решение. Применим к левой и правой частям уравнения с частными производными преобразование Фурье по переменной Получим обыкновенное неоднородное дифференциальное уравнение второго порядка с

нулевыми начальными условиями

Воспользуемся методом Дюамеля решения этой задачи Коши. Именно, решим вспомогательную задачу Коши.

Тогда решение исходной преобразованной задачи дается формулой

По формуле обращения преобразования Фурье

В теории функций Бесселя имеет место формула

Сделаем в этом равенстве замену

Теперь будем иметь

Сделаем в интеграле замену переменной ту откуда —

В силу интегральной формулы Фурье

Отсюда (в силу определения функции получаем

Двумерный случай (две пространственные переменные). Пример 3 [4, гл. IV, № 106]. Решить краевую задачу

Решение. Применяя преобразование Фурье к уравнению по переменным х и у и начальным условиям рассматриваемой задачи с учетом того, что

(последнее равенство устанавливается с помощью интегрирования по частям с использованием обращения в нуль на бесконечности по функции и ее частных производных получим задачу Коши

Решив эту задачу методом Дюамеля (или методом вариации произвольных постоянных), найдем

Применяя обратное преобразование Фурье, имеем

Подставляя сюда значения и обозначая придем к равенству

Вычислим четырехкратный несобственный интеграл, вводя полярные координаты соотношениями

Отсюда немедленно следует равенство

где Теперь имеем

Но справедливо равенство (интегральное представление функций Бесселя)

или (считая вещественным)

Трехмерный случай (три пространственные переменные). Пример 4 [4, гл. IV, № 107]. Решить краевую задачу

Решение. Применяя преобразование Фурье по переменным к уравнению и начальным условиям, получим задачу Коши

Решение указанной задачи (по аналогии с предыдущим) дается интегралом

По формуле обращения преобразования Фурье имеем

Для вычисления шестикратного интеграла перейдем к полярным координатам по формулам

(здесь 5 — угол между векторами Тогда

(кликните для просмотра скана)

Выполнив в последнем интеграле замену переменной откуда и переходя от поверхностного интеграла к объемному, окончательно получим

В заключение рассмотрим еще одну задачу на применение преобразования Фурье.

Пример 5 [4, гл. IV, № 108]. Решить краевую задачу (о колебаниях неограниченной пластины)

Решение. Применим преобразование Фурье по пространственным переменным к уравнению и начальным условиям. Предварительно найдем

Интегрируя по частям (с учетом обращения в нуль внеинтегральных членов), получим

Получим задачу Коши

Решение ее есть функция

Воспользовавшись обратным преобразованием Фурье, получим

(здесь мы воспользовались формулой и учли, что интегралы, содержащие равны нулю).

Выполним в полученном четырехкратном интеграле интегрирование по применяя формулы

Содержание данной заметки раскрывает вопросы как и почему работает известное всем энергетикам преобразование Фурье. Здесь мы постарались воздержаться от использования сложного понятийного аппарата, все использованные выкладки должны быть понятны каждому, кто хоть как-то овладел начальным уровнем университетского курса высшей математики. Для всех остальных не исключено понимание изложенного материала на интуитивном уровне.

В настоящее время преобразование Фурье широко используется как основа различных инструментов анализа аварийных осциллограмм. Примеры его использования в современных программах просмотра осциллограмм:

выделение действующего значения записанной электрической величины и её текущей фазы (рис. 1);
получение спектра – рис. 2;
построение векторной диаграммы (рис. 3);
построение временных годографов комплексных замеров электрических величин (к примеру, сопротивлений) – рис. 4.

Рис. 1. Иллюстрация применения преобразования Фурье для выделения действующего значения тока

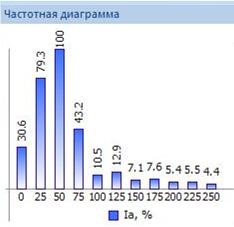
Рис. 2. Спектр как пример использования преобразования Фурье

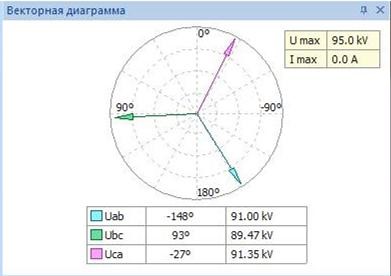
Рис. 3. Векторная диаграмма как пример использования преобразования Фурье

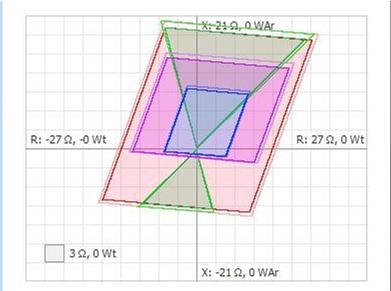
Рис. 4. Годограф сопротивления как пример использования преобразования Фурье

Таким образом, роль преобразования Фурье в анализе аварийных осциллограмм сложно переоценить. Далее перейдём к его сути.

Преобразование Фурье – это некий линейный оператор (см. рис. 5), который преобразует входной сигнал u(t) во временной области (t – это время) в сигнал U(f) в частотной области (f – это частота).

Предполагается, что входной сигнал u(t) состоит из набора (суммы) косинусоид следующего вида:

где f – частота; A – амплитуда; φ₀ – начальная фаза.

Далее идёт очень важное утверждение. В соответствии с известной формулой Эйлера, функция cos определяется как сумма двух комплексных экспонент:

где – мнимая единица.

Теперь можно внести уточнение: в общем случае преобразование Фурье предполагает, что входной сигнал u(t) состоит не из набора косинусоид, как это утверждалось чуть выше, а из набора комплексных экспонент.

Примечание: в преобразовании Фурье частота f – это частота комплексной экспоненты, а не косинусоиды.

Рассмотрим подробнее, из каких именно комплексных экспонент состоит косинусоида s(t). Первая экспонента e₁(t) описывает на комплексной плоскости равномерное движение точки по окружности с радиусом A/2 с постоянной угловой скоростью ω = 2πf – см. рис. 6.

Рис. 6. Первая комплексная экспонента, из которой состоит косинусоида

Вторая экспонента e₂(t) – это сестра-близнец первой экспоненты e₁(t), но в отличие от неё она описывает вращение точки по окружности в противоположную сторону – см. рис. 7. Также заметим, что графики e₁(t) и e₂(t) симметричны относительно действительной оси Re.

Рис. 7. Вторая комплексная экспонента, из которой состоит косинусоида

Итак, косинусоида с частотой f состоит из комплексной экспоненты с частотой f и комплексной экспоненты с частотой —f.

Такие периодические функции как синусоида, косинусоида и комплексная экспонента обладают очень важным с точки зрения преобразования Фурье свойством: их среднее значение (и интеграл тоже) на периоде равен нулю. Иными словами, если взять комплексную экспоненту с частотой f_x и усреднить её на периоде 1/f_x, то в результате усреднения мы получим нулевое значение. Это правило справедливо практически для всех комплексных экспонент с любой частотой f_x. Но в этом правиле есть одно исключение. Это экспонента с частотой f = 0 Гц, т.е. постоянная составляющая. В результате усреднения постоянной составляющей на любом интервале времени получается сама постоянная составляющая, т.е. она не обнуляется.

Посмотрим, как на рассмотренном правиле построено преобразование Фурье.

В качестве примера возьмём косинусоиду с частотой 50 Гц и амплитудой A. Мы знаем, что эта косинусоида состоит из двух комплексных экспонент с частотами -50 Гц и +50 Гц. Как эти составляющие расположены в области частот можно увидеть на рис. 8. Всего лишь два значения |U(f)| ненулевые – в точках -50 Гц и +50 Гц.

Рис. 8. Вид косинусоиды с частотой 50 Гц и амплитудой A в области частот

Если преобразование Фурье предназначено для преобразования сигнала во временной области u(t) в сигнал в частотной области U(f), то в случае косинусоиды u(t)=s(t) в качестве U(f) мы должны получить функцию, изображённую на рис. 8. Что такого можно сделать с s(t), чтобы на выходе получить |U(f)| как на рис. 8? Для простоты ограничимся не всей функцией |U(f)|, а только лишь одним её значением в точке f=50 Гц. В этой точке значение функции должно быть |U(50)|=A/2.

Итак, нам дана косинусоида s(t), заданное значение частоты f=50 Гц и информация о том, что при этой частоте должно выполняться равенство |U(50)|=A/2. Как нужно преобразовать s(t), чтобы на выходе преобразования было |U(50)|=A/2? Очевидно, что если просто усреднить косинусоиду s(t) на периоде 1/f=1/50=0,02 с, то на выходе мы получим ноль, т.е. |U(50)|=0. Поэтому просто усреднение на периоде не годится в качестве искомого преобразования. Попробуем другой вариант. Умножим s(t) на комплексную экспоненту с частотой -50 Гц:

В результате входящая в состав косинусоиды s(t) экспонента с частотой -50 Гц превратилась в экспоненту с частотой -100 Гц, а экспонента с частотой +50 Гц превратилась в комплексную экспоненту с частотой 0 Гц, т.е. в постоянную составляющую. Налицо смещение частот всех комплексных экспонент, входящих в состав входного сигнала, на значение -50 Гц. То, как после этого стали располагаться в области частот составляющие косинусоиды s(t) (теперь это сигнал s₁(t)), показано на рис. 9.

Рис. 9. Вид смещённой на -50 Гц косинусоиды в области частот

Далее усредним полученный сигнал s₁(t) на периоде 0,02 с. В результате усреднения входящая в состав s₁(t) экспонента с частотой -100 Гц () обнуляется, т.к. интервал времени 0,02 с равен двум её собственным периодам. В то же время вторая экспонента с частотой 0 Гц, входящая в состав s₁(t), не обнуляется, результат её усреднения равен A /2. Итак, усреднив сигнал s₁(t) на интервале времени 0,02 с, получим

Получили то, что хотели, а именно |U(50)|=A/2.

Собственно, в рассмотренных двух процедурах и заключается преобразование Фурье:

1) смещение частот всех комплексных экспонент, входящих в состав входного сигнала u(t), на значение —f_x для того, чтобы комплексная экспонента с частотой f_x превратилась в постоянную составляющую, тем самым приобретя, так сказать, иммунитет к обнулению через усреднение.

2) усреднение сигнала со смещёнными частотами на интервале времени, кратном периодам всех комплексных экспонент, входящих в состав сигнала u(t), с целью их обнуления (всех экспонент, кроме той, что превратилась в постоянную составляющую).

В общем случае в состав входного сигнала u(t) входит неограниченное число комплексных экспонент со всевозможными частотами. В этом общем случае процедура 2) работает только на интервале усреднения от -∞ до +∞, поскольку только такой интервал времени кратен любому периоду любой комплексной экспоненты. Итак, получили формулу для преобразования Фурье:

Приведённое объяснение преобразования Фурье помогает образному восприятию его сути. Более глубокое понимание этого преобразования и его модификаций (дискретное преобразование Фурье, оконное преобразование Фурье, ряд Фурье, вейвлет-преобразование и т.д.) достигается через понятие свертки функций.

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Просто и наглядно, почти на пальцах, я расскажу, а главное – покажу – что такое и как работает преобразование Фурье, без которого никак не обойтись в алгоритмах цифровой обработки сигналов. Вы убедитесь, что математика может быть не только сложной, но и красивой.

Автор не является профессиональным математиком, поэтому позволил себе существенные упрощения и, может быть, неточности. Однако, на основную идею это не должно было повлиять.

Наука | Научпоп

6.2K постов 69.4K подписчиков

Правила сообщества

ВНИМАНИЕ! В связи с новой волной пандемии и шумом вокруг вакцинации агрессивные антивакцинаторы банятся без предупреждения, а их особенно мракобесные комментарии — скрываются.

Основные условия публикации

- Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.

- Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.

- Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.

- Видеоматериалы должны иметь описание.

- Названия должны отражать суть исследования.

- Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.

Не принимаются к публикации

- Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.

- Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.

- Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.

Наказывается баном

- Оскорбления, выраженные лично пользователю или категории пользователей.

- Попытки использовать сообщество для рекламы.

- Многократные попытки публикации материалов, не удовлетворяющих правилам.

- Нарушение правил сайта в целом.

Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает @SupportComunity и общество пикабу.

– А вот скажите. есть ли прибор, который выполняет данное преобразование?

– Ну да. Наверное. Да. Есть.

– И как же он называется?

– Это. Дык. Преобразователь Фурье!

– Конечно. Логично. Естественно. Как же иначе. (поглаживая рукой методичку "Анализаторы спектра" к лабораторным работам) (с) из прошлой жизни. из давних сессий.

Для тех кто в теме хоть немного, видео, возможно, что то и обьясняет.
Для тех кто не в теме это просто бред сумашедшего. Какая оцифровка, какого двухтактного сигнала, зачем это вообще нужно и где применяется?
Если это должен быть научпоп, то это неуд

вот ещё для владеющих языком потенциального противника. весь канал - математический оргазм :)

Черд, у меня аж глазз задергался как вспомнил его реализацию в студенчестве на ассемблере.

"Если бы мне так рассказывали в школе. ", я бы нихрена не понял 👌

Я преподаватель физики и математики, знаю, как устроены ряды и различные преобразования, сам это объясняю людям, но видео было натужным прям

Да, конечно, "отвергаешь, предлагай", и уже выше кидали годные видосы, можно подсмотреть кое-какие ходы там, иначе выглядит понятным только для тех, кто уже это знает

Тоже что ли видосов напилить с разборами явлений мира физики и математики, нынче модно стало

Но автору всё равно респект за объяснение, кому-то будет полезным :)

Он разложил идеальную женщину в ряд Фурье (так звали старинного математика, славившегося большим числом любовниц — как уверяет исторический анекдот, они даже стояли в очереди к его дверям, откуда и возникло это выражение).

В результате у маркиза де Ломонозо появилось три подруги.

Одна — невероятная умница, проницательная, злая и острая на язык, прекрасный собеседник — но некрасивая.

Вторая была очень добра. Она писала замечательные письма — короткие, смешные и трогательные, любое из которых согревало душу. Она тоже была некрасива и вдобавок не особо умна.

А третья девушка, работавшая в кухне его загородного дома, была бесконечно прекрасным юным существом. Она не только не умела писать — она по сути не могла даже говорить, потому что изъяснялась на южном диалекте, и ее кое-как понимали одни лишь големы да служанки. Тут об уме и доброте говорить не приходилось вообще — в таком же объеме они свойственны, наверно, ящерице или стрекозе. Но она была безумно хороша и свежа.

Де Ломонозо обустроил свою жизнь следующим образом: ежедневно пил чай с первой из девушек, в минуты одиночества перекидывался записками со второй, а по ночам обнимал третью.

Но в своем воображении он сплавлял их в одно-единственное совершенное существо, обладавшее умом первой, отзывчивостью второй и красотою третьей. Разговаривая с первой, он щурился и представлял себе на ее месте третью, а обнимая ночью третью, вспоминал трогательное письмо, полученное вечером от второй, и так далее.

Посмотрел всё видео.

Чувствую себя как тот медведь из анекдота сейчас. Чтобы потом не было "ты знаешь правило" - вот он.

Попали как-то раз в яму медведь, волк и лось. Сидя день, два, на третий не вытерпели и говорят лосю, дескать жрать охота, невмоготу, готовься. Ну лось и говорит:

- Жрите, что же делать. Тока есть у меня просьба, на заднице у меня написано завещание, прочтите перед моей смертью.

Волк с медведем сунулись читать, а лось как даст копытами. Волка насмерть, а медведь чуть живой лежит и причитает:

- Ну ладно волк, он тупой же, но я-то, я-то куда полез? Я же читать не умею!

Это гениально! Если это кому-то поможет вышку и прочувствовать и понять. Я от фамилии Фурье помню только ряды, и что они сходящиеся бывают))))

Света, 5 лет матфака и магистратура))))

Я же не один там вижу жопу, да?

глоток свежего воздуха на зигабу

Можно еще здесь посмотреть. И здесь имхо лучше объясняют. Но нужно чуть чуть в инглиш.

Сейчас уже подзабылось,но в универе прекрасно доносил преподаватель,что такое свертки,преобразования фурье итд.

Просто и наглядно, почти на пальцах, я расскажу.

Где рассказ то, а?

Пост есть говно! Потому что без описания. Мы не обязаны иметь звук в наличии.

Пос говно не о чём.

Посмотрел 5 минут и не понял где там преобразование Фурье.

Суть преобразования Фурье в рядах Фурье, по аналогии с рядами Тейлара. Любой сигнал можно представить в виде суммы синусов. Как и любую непрерывную кривую можно преставить в виде суммы дуг окружностей, что по сути одно и тоже.

А преобразование фурье - это получение спектра сигнала. Разложение ряда по целым частотам, по их амплитуде.

Ряды бесконечные, но можно считать только первые коэффициенты, так как остальные добавляют все меньше точности. Поэтому эти расчеты может просчитат даже калькулятор. Радуга - это аналоговое разложение Фурье.

На редкость занудный голос.

Самое важное было сказано в 1 предложении, которое я не понял. Как из этих сложных неупорядоченных фигур с помощью центра масс находятся пики?

У меня преобразование Фурье на пальцах. Доктор, это лечится?

Ни хуя не понятно, но очень интересно.

Можно для тех кто в танке разъяснить где это на практике применяется?

Волки и зайцы в графиках и портретах

Ну есть хищники, ну есть жертвы. Чего тут такого-то? Если, конечно, это не хищники из серии одноименных фильмов. Подумаешь. Вроде бы очевидно, что хищник поедает жертв, на то они и жертвы. Однако, даже такие, несколько спонтанные явления можно объяснить математически.

Рассмотрим самый простой вариант. В роли хищника будут волки, в роли жертвы – зайцы. Зайцам хватает растений. Все животные живут на ограниченной территории, но трава успевает отрастать, так что ушастые не бедствуют. А теперь уберите от экрана женщин, детей и слабонервных. Начинаем мы с того, что количество зайцев относится к количеству волков 3:1. Система живет, зайцы прыгают, а волка ноги кормят. Обе популяции растут и радуются их гипотетической жизни. Затем численность хищников достигает некоторой цифры, они, как и любые организмы, питаются, численность зайцев идет на убыль. Дело все в том, что потребление становится так велико, что популяция просто не успевает восстановиться. Кстати говоря, не вся энергия переходит хищникам от зайца, а только 10%, поэтому один волк ест несколько зайцев. Так как еды становится мало, то вполне логично, что и хищники начинают гибнуть. Продолжается это до тех пор, пока количество жертв не сможет выйти на тот уровень, что популяция росла. До сего момента хищники убывают. Зато потом в рост идут и волки, и зайцы. И вот популяции снова растут, солнце светит, жизнь прекрасна. А потом волков становится много, они едят зайцев, зайцев становится мало, волки тоже мрут. Где-то Вы это уже видели? Я скажу Вам где: несколько строчек назад. Не то чтобы это день сурка, просто развивается все циклично.

А как это вообще связано с компьютером? Программа, в которую вбивают данные для уравнения Лотки – Вольтерра может построить графики, которые, собственно, и донесут мое повествование. Увидеть можно график функции, фазовый портрет, который представляет из себя концентрические замкнутые кривые вокруг стационарной точки, и фазовую траекторию – тот же фазовый портрет, только 3D ( см. графики 1)

Кроме такой идеализированной системы, могут быть внесены правки. Например, можно добавить элемент конкуренции внутри одного вида. Случалось ли Вам забрать последнюю печеньку из пачки? А волки могут друг друга и загрызть. А зайцы могут употребить свое же потомство. Такова жизнь. Зато картина выходит интереснее. На графике функции колебания не одинаковы, их амплитуда убывает до некоторого количества так, как убывает число хищников и жертв, потому что внутривидовая конкуренция дополнительно снижает численность каждого вида до тех пор, пока количество и тех, и других не придет к какому-то числу, при котором животные могут разбрестись по территории так, что внутривидовая конкуренция не будет так сильно их уничтожать. На фазовом портрете это будет выглядеть не как замкнутая кривая, а как то, что мы видим, сливая воду, все будет стремиться к этой стационарной точке, точке равновесия и покоя. (см графики 2)

Если бы стартом нашей гипотетической системы была как раз-таки стационарная точка, то все было бы наоборот: популяции бы росли. На графике функции амплитуды бы увеличивались с течением времени, а на фазовом портрете прямая бы не закручивалась в центр, а раскручивалась из него, иллюстрируя рост популяций. (см. графики 3)

Существуют и другие модели, которые не так восприимчивы к переменам. Такой является модель Холлинга – Тэннера. Если бы мы взяли другое отношения жертв к хищникам, например, их было бы поровну, то система бы стремилась вернуться в устойчивое состояние. С течением времени, зайцев по отношению к волкам стало бы 3:1. Будь у нас ровно два зайца и два волка, то одному хищнику бы явно не хватило жертв. Зато зайцы быстро размножаются. Несмотря на то, что их поедают, популяция все равно бы успевала вырасти. А потом система бы пришла к тому, что описывалась ранее. На графике мы бы увидели увеличение амплитуды, а затем ровные, одинаковые периоды. А на фазовом портрете у таких моделей есть предельные циклы. Прямая бы раскручивалась от точки 2;2 до этого предельного цикла. А прямая из стационарной точки 3:1 скручивалась бы к циклу. (см. графики 4)

Если принять, что в уравнении параметры не константы, а коэффициенты, зависящие от числа жертв, то картина будет иной. Возьмем два параметра, которые обратно зависят друг от друга. Пусть это будет насыщаемость хищника и скорость его размножения. Если насыщаемость высокая, то зайцев нужно меньше. Так как между параметрами обратная зависимость, то потомства у волков производится медленно. Обе популяции тогда будут постепенно уменьшаться до стабилизации на каком-то ненулевом уровне. На графике амплитуда будет уменьшаться, в конце будет практически ровной прямой. Фазовый портрет проиллюстрирует то же самое: прямая будет скручиваться к некоторой ненулевой стабильной для системы точке. (см. графики 5)

Фото: proglib.io

С учетом экспоненциального роста объемов аудиовизуальной информации, становится все актуальнее вопрос о поиске методов эффективного преобразования и сжатия этой информации. Один из методов преобразования разработал еще 200 лет назад математик Жан Батист Жозеф Фурье.

В чем суть метода Фурье для сжатия информации?

Существует большое число технологий и математических методов для сжатия изображений. Однако каким бы ни был алгоритм, используемый для сжатия информации (далее будем делать практический разбор на примере сжатия изображений, это наиболее наглядно и просто для восприятия), принцип алгоритма всегда будет заключаться в следующем: найти и описать закономерности в массиве информации.

По сути любое изображение — это массивы информации. Любое видео — это массивы информации. Аудиоролик или большой объем данных для машинного обучения — это тоже массивы с информацией. Не так важно, какая технология используется в том или ином случае для сжатия. Гораздо важнее, какие алгоритмы лежат в ее основе.

Итак, алгоритмы сжатия сводятся к поиску закономерностей в массиве данных. И чем больше удастся выявить закономерностей, тем больше будет избыточности, и тем меньший объем информации останется после сжатия.

Можем легко увидеть это на простейшем примере. Откроем любую программу для рисования изображений (например, стандартный Paint). И закрасим всю область одним единственным цветом. Сохраним изображение. Размер изображения — 1.28 Кб

Теперь создадим изображение такого же размера в той же программе, но и использованием разных цветовых палитр и композиций. Размер изображения сразу увеличивается до 9 Кб.

Это наглядный пример работы методов сжатия изображений. В данном случае кодировщик разглядел закономерность в том, что все пиксели первого изображения имеют одинаковую яркость и цвет, поэтому изображение получилось в несколько раз “легче” второго, где таких закономерностей меньше. Простой пример, показывающий важность использования методов сжатия информации. В частности, в формате JPEG для сжатия используется именно метод Фурье.

Фурье начал разработку своего метода еще в конце 18 века. Метод Фурье — это один из самых распространенных методов решения уравнений с частными производными, показывающий высокую практическую и теоретическую эффективность. Сам метод часто можно встретить под другими названиями: метод разделения переменных либо метод собственных функций.

Основной базой для сжатия информации является представление функций тригонометрическими рядами Фурье. Сами ряды Фурье являются способом представления произвольной сложной функции путем суммирования нескольких простых функций.

Как это работает на практике на примере аппроксимации изображений?

Аппроксимация — это научный подход замены одних объектов в массиве данных другими. Конечным результатом аппроксимации может быть в том числе и сжатие данных, которое нас интересует.

Давайте представим монохромное (черно-белое изображение) размером l на l пикселей в виде сеточной функции ƒ(i, j), где:

i, j — координаты конкретного пикселя нашего монохромного изображения;
i, j могут принимать значение от 1 до l (количество пикселей по одной стороне в нашем изображении).

Значением функции является яркость конкретного пикселя. Значение яркости меняется от 0 до 255. В процессе сжатия монохромного изображения функция яркости будет подвержена аппроксимации частичной суммы дискретного разложения по косинусам.

На первом этапе в процессе сжатия изображения используются дискретные аналоги рядов Фурье.

На втором этапе уже аппроксимированное изображение проходит этап квантования — это процесс деления непрерывного динамического диапазона значений яркости на ряд дискретных уровней при цифровой обработке изображения.

Третьим этапом является группировка данных.

Четвертый и последний этап сжатия — архивирование. Именно по этому принципу работает, например, технология JPEG.

Практическая реализация. Прикладное применение метода

Использование метода Фурье получило широкое практическое применение, и используется программистами и разработчиками для:

Сжатия изображений;
Сжатия видео;
Сжатия аудио;
Оперирования большими объемами данных;
Прогнозирования событий (в частности для аппроксимации временных рядов);
Обучение нейронных сетей, искусственного интеллекта, data science.

На сегодняшний день используются 3 подхода для практического использования метода Фурье. Рассмотрим их также на примере работы с изображением.

Подход первый. Этот подход мы уже рассмотрели в примере ранее. Его суть заключается в аппроксимации изображения как сеточной функции с двумя переменными. Для применения подхода необходим дискретный аналог кратного ряда Фурье. Этот способ не нашел широкого и повсеместного практического применения, поскольку подразумевает использования больших количеств машинных ресурсов и времени.

Подход второй. Суть подхода состоит в разбиении изображения на отдельные строки пикселей, после чего происходит отдельная аппроксимация каждой конкретной строки.
Этот подход в практическом смысле значительно эффективнее предыдущего, потому что здесь обрабатываются функции одной переменной, а не двух.

Подход третий. Суть подхода заключается в разбиении изображений на отдельные прямоугольные блоки, после чего осуществляется последовательная аппроксимация каждого блока по-отдельности.

Такой подход позволяет лучше всего бороться с эффектом Гиббса (ситуацией, когда изображение становится слишком “шумным”).

Пример реализации метода Фурье для сжатия изображений

В качестве примера реализации на практике метода Фурье рассмотрим монохромное изображение. На первом рисунке представлено исходное изображение. На втором после аппроксимации было сохранено ⅔ значений из массива данных изображения. На третьем изображении было сохранено ⅓ значений из массива данных изображения. Как вы можете видеть, качество изображения в третьем случае заметно ухудшилось, это и есть эффект Гиббса, о котором говорилось ранее.

Однако обратите внимание, что во втором случае изображение после сжатия сохранило качество и четкость, видны плавные переходы пикселей, а это означает, что при должном подходе метод Фурье отлично справляется со своими задачами.

Выводы

Исходя из полученной информации и изучения практических аспектов его применения, можно сделать вывод, что метод Фурье и за две сотни лет не утратил своей актуальности. А эффективность метода подтверждается его широким и повсеместным использованием для сжатия больших объемов информации, будь то аудиовизуальная информация или большие массивы данных.

Читайте также: