Параметр лямбда в гребневой регрессии

Обновлено: 07.07.2024

Быстренько назовите пять алгоритмов машинного обучения. Вряд ли вы назовете много алгоритмов регрессии. В конце концов, единственным широко распространенным алгоритмом регрессии является линейная регрессия, главным образом из-за ее простоты.

Однако линейная регрессия часто неприменима к реальным данным из-за слишком ограниченных возможностей и ограниченной свободы маневра. Ее часто используют только в качестве базовой модели для оценки и сравнения с новыми подходами в исследованиях.

Перевели статью, автор которой описывает 5 алгоритмов регрессии. Их стоит иметь в своем наборе инструментов наряду с популярными алгоритмами классификации, такими как SVM, дерево решений и нейронные сети.

1. Нейросетевая регрессия

Теория. Нейронные сети невероятно мощные, но их обычно используют для классификации. Сигналы проходят через слои нейронов и обобщаются в один из нескольких классов. Однако их можно очень быстро адаптировать в регрессионные модели, если изменить последнюю функцию активации.

Каждый нейрон передает значения из предыдущей связи через функцию активации, служащую цели обобщения и нелинейности. Обычно активационная функция — это что-то вроде сигмоиды или функции ReLU (выпрямленный линейный блок).

Источник. Свободное изображение

Но, заменив последнюю функцию активации (выходной нейрон) линейной функцией активации, выходной сигнал можно отобразить на множество значений, выходящих за пределы фиксированных классов. Таким образом, на выходе будет не вероятность отнесения входного сигнала к какому-либо одному классу, а непрерывное значение, на котором фиксирует свои наблюдения нейронная сеть. В этом смысле можно сказать, что нейронная сеть как бы дополняет линейную регрессию.

Нейросетевая регрессия имеет преимущество нелинейности (в дополнение к сложности), которую можно ввести с сигмоидной и другими нелинейными функциями активации ранее в нейронной сети. Однако чрезмерное использование ReLU в качестве функции активации может означать, что модель имеет тенденцию избегать вывода отрицательных значений, поскольку ReLU игнорирует относительные различия между отрицательными значениями.

Это можно решить либо ограничением использования ReLU и добавлением большего количества отрицательных значений соответствующих функций активации, либо нормализацией данных до строго положительного диапазона перед обучением.

Реализация. Используя Keras, построим структуру искусственной нейронной сети, хотя то же самое можно было бы сделать со сверточной нейронной сетью или другой сетью, если последний слой является либо плотным слоем с линейной активацией, либо просто слоем с линейной активацией. (Обратите внимание, что импорты Keras не указаны для экономии места).

Проблема нейронных сетей всегда заключалась в их высокой дисперсии и склонности к переобучению. В приведенном выше примере кода много источников нелинейности, таких как SoftMax или sigmoid.

Если ваша нейронная сеть хорошо справляется с обучающими данными с чисто линейной структурой, возможно, лучше использовать регрессию с усеченным деревом решений, которая эмулирует линейную и высокодисперсную нейронную сеть, но позволяет дата-сайентисту лучше контролировать глубину, ширину и другие атрибуты для контроля переобучения.

2. Регрессия дерева решений

Из-за специфической и высокодисперсной природы регрессии просто как задачи машинного обучения, регрессоры дерева решений следует тщательно обрезать. Тем не менее, подход к регрессии нерегулярен — вместо того, чтобы вычислять значение в непрерывном масштабе, он приходит к заданным конечным узлам. Если регрессор обрезан слишком сильно, у него слишком мало конечных узлов, чтобы должным образом выполнить свою задачу.

Следовательно, дерево решений должно быть обрезано так, чтобы оно имело наибольшую свободу (возможные выходные значения регрессии — количество конечных узлов), но недостаточно, чтобы оно было слишком глубоким. Если его не обрезать, то и без того высокодисперсный алгоритм станет чрезмерно сложным из-за природы регрессии.

Реализация. Регрессия дерева решений может быть легко создана в sklearn:

Поскольку параметры регрессора дерева решений очень важны, рекомендуется использовать инструмент оптимизации поиска параметров GridCV из sklearn, чтобы найти правильные рекомендации для этой модели.

При формальной оценке производительности используйте тестирование K-fold вместо стандартного train-test-split, чтобы избежать случайности последнего, которая может нарушить чувствительные результаты модели с высокой дисперсией.

Бонус: близкий родственник дерева решений, алгоритм random forest (алгоритм случайного леса), также может быть реализован в качестве регрессора. Регрессор случайного леса может работать лучше или не лучше, чем дерево решений в регрессии (в то время как он обычно работает лучше в классификации) из-за тонкого баланса между избыточным и недостаточным в природе алгоритмов построения дерева.

3. Регрессия LASSO

Теория. Метод регрессии лассо (LASSO, Least Absolute Shrinkage and Selection Operator) — это вариация линейной регрессии, специально адаптированная для данных, которые демонстрируют сильную мультиколлинеарность (то есть сильную корреляцию признаков друг с другом).

Она автоматизирует части выбора модели, такие как выбор переменных или исключение параметров. LASSO использует сжатие коэффициентов (shrinkage), то есть процесс, в котором значения данных приближаются к центральной точке (например среднему значению).

Процесс сжатия добавляет регрессионным моделям несколько преимуществ:

Более точные и стабильные оценки истинных параметров.
Уменьшение ошибок выборки и отсутствия выборки.
Сглаживание пространственных флуктуаций.

Вместо того чтобы корректировать сложность модели, компенсируя сложность данных, подобно методам регрессии с высокой дисперсией нейронных сетей и дерева решений, лассо пытается уменьшить сложность данных так, чтобы их можно было обрабатывать простыми методами регрессии, искривляя пространство, на котором они лежат. В этом процессе лассо автоматически помогает устранить или исказить сильно коррелированные и избыточные функции в методе с низкой дисперсией.

Регрессия лассо использует регуляризацию L1, то есть взвешивает ошибки по их абсолютному значению. Вместо, например, регуляризации L2, которая взвешивает ошибки по их квадрату, чтобы сильнее наказывать за более значительные ошибки.

Такая регуляризация часто приводит к более разреженным моделям с меньшим количеством коэффициентов, так как некоторые коэффициенты могут стать нулевыми и, следовательно, будут исключены из модели. Это позволяет ее интерпретировать.

Реализация. В sklearn регрессия лассо поставляется с моделью перекрестной проверки, которая выбирает наиболее эффективные из многих обученных моделей с различными фундаментальными параметрами и путями обучения, что автоматизирует задачу, которую иначе пришлось бы выполнять вручную.

4. Гребневая регрессия (ридж-регрессия)

Теория. Гребневая регрессия или ридж-регрессия очень похожа на регрессию LASSO в том, что она применяет сжатие. Оба алгоритма хорошо подходят для наборов данных с большим количеством признаков, которые не являются независимыми друг от друга (коллинеарность).

Однако самое большое различие между ними в том, что гребневая регрессия использует регуляризацию L2, то есть ни один из коэффициентов не становится нулевым, как это происходит в регрессии LASSO. Вместо этого коэффициенты всё больше приближаются к нулю, но не имеют большого стимула достичь его из-за природы регуляризации L2.

В лассо улучшение от ошибки 5 до ошибки 4 взвешивается так же, как улучшение от 4 до 3, а также от 3 до 2, от 2 до 1 и от 1 до 0. Следовательно, больше коэффициентов достигает нуля и устраняется больше признаков.

Однако в гребневой регрессии улучшение от ошибки 5 до ошибки 4 вычисляется как 5² − 4² = 9, тогда как улучшение от 4 до 3 взвешивается только как 7. Постепенно вознаграждение за улучшение уменьшается; следовательно, устраняется меньше признаков.

Гребневая регрессия лучше подходит в ситуации, когда мы хотим сделать приоритетными большое количество переменных, каждая из которых имеет небольшой эффект. Если в модели требуется учитывать несколько переменных, каждая из которых имеет средний или большой эффект, лучшим выбором будет лассо.

Реализация. Гребневую регрессию в sklearn можно реализовать следующим образом (см. ниже). Как и для регрессии лассо, в sklearn есть реализация для перекрестной проверки выбора лучших из многих обученных моделей.

Определить оптимальный метод преобразования сигнала из пяти предложенных. Продемонстрировать результаты всех измерений.

Теория по данной теме:

Первый метод, который мы рассмотрим-метод наименьших квадратов (МНК)

Метод наименьших квадратов — один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Метод наименьших квадратов применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина прямой или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятности; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Большие затруднения представляются при определении из наблюдений величин, которые не могут быть измерены непосредственно. Если, например, желают определить элементы орбиты планеты или кометы, то светила эти наблюдаются несколько раз, и в результате получают лишь координаты их (склонение и прямое восхождение) в известные времена; самые же элементы выводятся затем решением уравнений, связывающих наблюдаемые координаты с элементами орбиты планеты или кометы. При этом, если бы число уравнений равнялось числу неизвестных, то для каждой неизвестной получилась бы одна определенная величина; если же число уравнений больше числа неизвестных, то, вследствие ошибок наблюдений, результаты решений отдельных групп этих уравнений в различных сочетаниях оказываются не совсем согласными между собой.Классический метод наименьших квадратов в ряде случаев, как известно, является не устойчивым, что приводит к большим погрешностям при обработке сигнала. Поэтому кроме классического метода МНК используют и его модификации. На пример:

-метод QR разложения;

Точность решения зависит от:

2. Вида весовой функции

Метод гребневой регрессии

В методе гребневой регрессия оптимальное значение коэффициента регуляризации определяется из условия плавности графиков зависимости компонент вектора решения от величины коэффициента регуляризации.

Сравнение полученного решения с точным значением возможно только в модельном эксперименте. В натуральном эксперименте этого сделать нельзя, так как неизвестно точное решение.

По этому выбрать оптимальное значение коэффициента регуляризации в этом методе не представляется возможным. Для выбора оптимального значения необходима дополнительная информация.

Рассмотрим систему уравнений

где - действительная, симметричная, неотрицательно определенная матрица. Собственные числа такой матрицы попарно различны. Определитель матрицы равен . Если l_n=0, то матрица будет вырождена.

Рассмотрим матрицу , где r>0. Спектр собственных чисел этой матрицы имеет вид , а определитель равен

т.е. матрица не вырождена. Следовательно, система уравнений

имеет решение. Если r

Метод Тихонова

Регуляризация Тихонова (в английской литературе ridge regression) для интегральных уравнений позволяет балансировать между соответствием данным и маленькой нормой решения. L2 = Σ(yt-y)2 + λ*Σ(ai)2

известно[1], что это уравнение является некорректным по Адамару, т.е. погрешность решения этого уравнения, даже при малых погрешностях y(t), может быть очень большой.

Для решения подобных задач применяется метод регуляризации Тихонова, а сами задачи называются корректными по Тихонову. Положим, что y(t) содержит случайную погрешность x(t). Тогда каждой реализации случайной погрешности x(t) будет соответствовать свое решение интегрального уравнения, очевидно, что среди этих решений есть и такие которые имеют малую погрешность. Для того чтобы из этого множества решений выбрать те которые устраивают нас по точности необходимо использовать какую либо дополнительную информацию и виде решения.

Поскольку при численном решении интегрального уравнения оно заменяется системой линейных уравнений, то дальнейшие выкладки будут приведены для случая системы линейных уравнений.

Представим интегральное уравнение в виде

x(t)- случайная функция (погрешность измерения).

Положим, что известна погрешность измерения вектора (например по результатам тестирования установки) т.е. известно значение величины

где х * - точное решение уравнения.

Обозначим через d квадрат невязки решения, равный

и будем искать решение уравнения, имеющее минимальную норму при условии, что квадрат невязки решения равно x 2 . Следовательно, решение исходной задачи сведено к решению вариационной задачи на условный экстремум, которая может быть решена методом неопределенных множителей Лагранжа.

Фильтр Калмана

Фильтр Калмана это эффективный рекурсивный фильтр, который оценивает состояние линейной динамической системы по серии неточных измерений. Он используется в широком спектре задач от радаров до систем технического зрения, и является важной частью теории систем.

Фильтры Калмана основываются на линейных динамических системах, дискретизированных по времени. Они моделируются цепями Маркова, построенными на линейных операторах с внесенными погрешностями с нормальным Гауссовым распределением. Состояние системы считается вектор из действительных чисел. При каждом шаге по времени, линейный оператор применяется к вектору состояния системы, добавляется некоторая погрешность и опционально некоторая информация об управляющих воздействиях на систему, если таковая известна. После чего другим линейным оператором с другой погрешностью добавляется видимая информация о состоянии системы. Фильтр Калмана можно рассматривать в качестве аналога скрытым моделям Маркова, с тем ключевым отличием, что переменные, описывающие состояние системы, являются элементами бесконечного множества действительных чисел (в отличие от конечного множества пространства состояний в скрытых моделях Маркова). Кроме того, скрытые модели Маркова могут работать с произвольными распределениями для следующих значений переменных состояния системы, в отличие от модели стандартного Гауссового распределения, поддерживаемого фильтрами Калмана.

Фильтр Калмана является разновидностью рекурсивного фильтра. Это означает, что только результат предыдущей итерации фильтра (в виде оценки состояния системы и оценки погрешности определения этого состояния) и текущие наблюдения нужны для расчета текущего состояния системы. В отличие от пакетных фильтров не требуется хранение никакой истории наблюдений. В следующем дальше тексте запись означает оценку состояния системы в момент времени n при учете наблюдений (измерений) с начала работы фильтра и по момент времени m включительно.

Состояние фильтра содержится в двух переменных:

, оценочное состояние системы в момент времени k, которое получено на основании начального состояния системы и всех наблюдений по момент времени k включительно;
, матрица ковариаций этого состояния, включающая в себя оценку дисперсий погрешности вычисленного состояния и уровни ковариаций, показывающих выявленные взаимосвязи между параметрами состояния системы.

Итерация фильтра Калмана делится на две фазы: Предсказание и Учет наблюдений. Фаза предсказания использует вычисленное на предыдущем шаге состояние для получения через модель системы оценочного состояния на текущем шаге. В фазе учета наблюдения информация об измерениях произведенных на текущем шаге используется для уточнения информации о состоянии системы, что делает её в результате (надеемся) более точной.

Практическая часть:

МНК

Выберем 1 функцию и 1 весовую. Шум не добавляем. Изучим полученный результат.

Из всех полученных результатов только один метод МНК- QR-разложение дал правильный результат. Остальные варианты даже близко не подходят к решению. Рассмотрим 2 функцию.

Как видно из графиков 2 функции, не сработал ни один из методов МНК. QR-разложение лишь в конце стало приближаться к норме. Даже несмотря на низкий уровень шума, решение методом МНК не приближается к истинному.

Если мы увеличим уровень шума, то решение абсолютно расходится.

Вывод: МНК крайне неточный метод, в редких случаях лишь QR-разложение дает положительный результат. В общем случае точность данного метода зависит от вида самой функции, а также весовой, и уровня шума.

Метод гребневой регрессии:

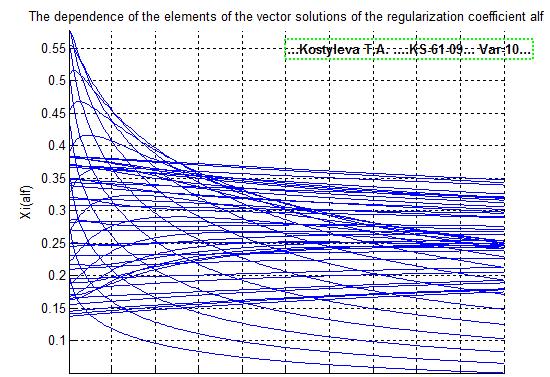
В данном методе нам предлагается самим выбрать коэффициент регуляризации. Сначала возьмем данный, который равен 0.1. Решение при этом не получилось

Попробуем менять коэффициент и понаблюдаем, как будет меняться результат.

Уменьшив коэффициент регуляризации решение стало стремиться к оптимальному. Попробуем увеличить ещё

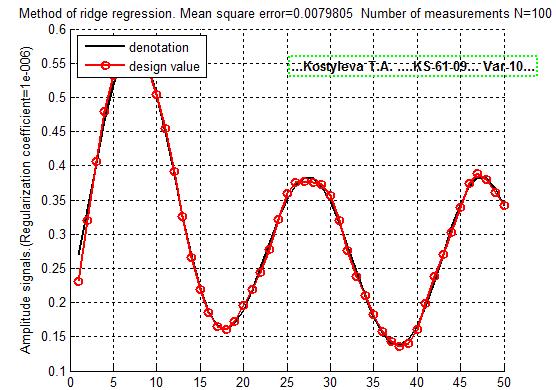
Увеличив К до 0.000001 мы почти в плотную подобрались к точному решению.

Используя третью весовую функцию нам сразу же удалось найти решение и подходящий коэффициент регуляризации, он равен 0.01

Вывод: Точность решения методом гребневой регрессии зависит от коэффициента регуляризации. Важно найти оптимальное значение, чтобы попасть именно в нужное решение.

Метод Тихонова

При очень низком уровне шума, решение методом Тихонова получилось довольно точным. Возьмем 2 весовую функцию, и немного увеличим шум.

После увеличения уровня шума-решение заметно ухудшилось.

Сильно уменьшив уровень шума в 3 весовой функции, мы получили достаточно неплохой результат, хоть и не совсем точный.

Вывод: Точность решения зависит как от уровня шума правой части, так и от вида весовой функции. Метод Тихонова сильно сглаживает решение. Главный недостаток-погрешность растет с увеличением количества измерений из-за постоянных округлений.

Итеративный МНК

Как и классический МНК, итеративный не дает нам точного решения.

Увеличив число итераций и немного уменьшив шум, мы получаем вполне приличный результат. ИМНК не полностью справился с задачей, но увеличив число итераций ещё на пару порядков, результат будет точнее.

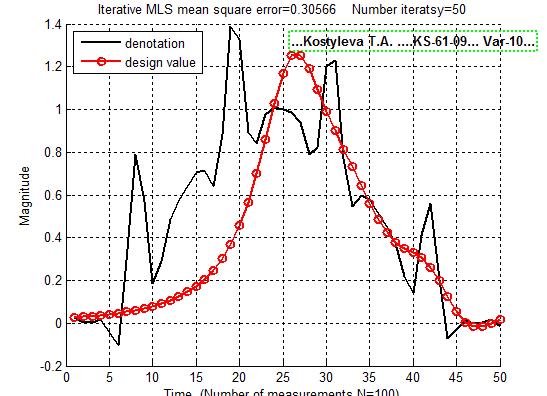
А вот со 2 функцией итеративный МНК дал очень плохой результат, хотя уровень шума был достаточно низким.

Увеличив число итераций до 1000, решение стало больше напоминать верное, но оно по прежнему далеко от идеала.

Но сделав число итераций очень большим (около 3000), решение снова уходит от нас. Это происходит из-за накопленных ошибок.

Вывод: Метод ИМНК гораздо точнее классического МНК, но из-за накапливания погрешностей его также нельзя назвать точным.

Фильтр Калмана:

Следуя указанным значениям в примере, мы не можем судить о правильности метода из-за недостаточного числа итераций. Увеличим их

Приняв 1000 за количество итераций, наше решение становиться практически точным.

А уже на 2 весовой, метод фильтра Калмана не сработал даже при большом числе итераций.

Во 2 функции и в 3 весовой мы получаем довольно неплохой результат, учитывая средний уровень шума и небольшое число итераций.

Вывод: Метод Калмана является довольно точным. Его точность зависит от начального приближения и от количества итераций и уровня шума.

Общий вывод:

Выполнив данную лабораторную работу, можно с уверенностью сказать что МНК является самым неочным, в метод фильтра Калмана, наоборот. Даже при высоком уровне шума и и среднем числе итераций, мы получаем вполне приемлимые данные.

Очень удобным визуальным способом оценки адекватности регрессионной модели является анализ графика опытных и полученных по регрессионному уравнению значений зависимой переменной. Он строится при помощи кнопки Predictedvs. observedокна анализа остатков.

Следует заметить, что мы имеем очень небольшое число данных – всего 12. Поэтому мы используем графические методы оценки адекватности модели. В сложных задачах графические и статистические методы оценки адекватности должны естественно дополнять друг друга.

Кнопка Redundancy предназначена для поиска выбросов. Выбросы – это остатки, которые значительно превосходят по абсолютной величине остальные. Выбросы дают данные, которые являются не типичными по отношению к остальным данным и требуют выяснения причин их возникновения. Выбросы должны исключаться из обработки, если они вызваны ошибками измерения. Для выделения выбросов, имеющихся в регрессионных остатках, предложены следующие метрики:

Расстояние Р.Д. Кука (Cook's Distance) показывает расстояние между коэффициентами уравнения регрессии после исключения из обработки каждой точки данных. Большое значение показателя Кука указывает на сильно влияющее наблюдение.
Расстояние Махаланобиса (Mahalanobis Distance) показывает, насколько каждое наблюдение отклоняется от центра статистической совокупности.

Корреляционный и дисперсионный анализ модели

Частная корреляция – это корреляция между двумя переменными, когда одна или больше из оставшихся переменных удерживаются на постоянном уровне. Частные коэффициенты корреляции, как и парные, могут принимать значения от –1 до +1. Кнопка Partialcorrelations окна результатов регрессионного анализа позволяет просмотреть частные коэффициенты корреляции (Partial Cor.) между переменными.

В идеальной регрессионной модели независимые переменные вообще не коррелируют друг с другом. В самом деле, если две независимые переменные сильно коррелированы с откликом и друг с другом, то достаточно включить в уравнение только одну из них. Обычно включают ту переменную, значения которой легче и дешевле измерять.

Сильная взаимная коррелированность независимых переменных в нашем уравнении затрудняет анализ влияния отдельных факторов на зависимую переменную. Сильная коррелированность переменных в моделях, разрабатываемых для промышленных приложений, является частым явлением. Это приводит к увеличению ошибок уравнения, уменьшению точности оценивания. Общая эффективность использования регрессионной модели снижается. Поэтому выбор независимых переменных, включаемых в регрессионную модель, необходимо проводить очень тщательно.

Кнопка ANOVA (Overallgoodnessoffit) окна результатов регрессионного анализа позволяет ознакомиться с результатами дисперсионного анализа уравнения регрессии.

В строках таблицы дисперсионного анализа уравнения регрессии записаны источники вариации: Regress. – обусловленная регрессией, Residual – остаточная, Total – общая. Значения столбцов таблицы: Sums of Squares – сумма квадратов, df – число степеней свободы, Mean Squares – среднеквадратическое значение, F – значение F-критерия, p-level – вероятность нулевой гипотезы для F-критерия. Видим, что F-критерий полученного уравнения регрессии значим на 0,05-уровне. Вероятность нулевой гипотезы (p-level) значительно меньше 0,05, что говорит об общей значимости уравнения регрессии.

Кнопка Predictdependentvariableпозволяет рассчитать по полученному регрессионному уравнению значение зависимой переменной по значениям независимых переменных, которые необходимо ввести в появляющемся диалоговом окне.

Кнопка Descriptivestatisticsпозволяет просмотреть описательные статистики и корреляционную матрицу с парными коэффициентами корреляции переменных, участвующих в регрессионной модели.

Фиксированная нелинейная регрессия

В некоторых случаях нелинейные модели с помощью специальных линеаризирующих преобразований могут быть преобразованы в линейные. Рассмотрим порядок нахождения коэффициентов уравнений нелинейной регрессии, которые через преобразования переменных могут быть приведены к линейной модели. В качестве примера рассмотрим экономические показатели некоторого предприятия за три квартала текущего года. Предположим, что необходимо определить, как влияют на полученную прибыль (y) доходы (x₁), фонд оплаты труда рабочих (x₂) и накладные расходы (x₃). Полученная формула, например, позволит составить прогноз на следующий месяц и оценить значимость каждого фактора.

Решается задача регрессии. Применяется линейная модель (вообще говоря, один из признаков полагается константным для того, чтобы аппроксимирующая гиперплоскость не обязательно проходила через нуль, я не знаю, почему это практически всюду опускается): " width="" height="" />
. В изначальной постановке полагается, что вектор " width="" height="" />
находится методом Обычных Наименьших Квадратов (ОНК): ^(f(x_,\beta )-y_)^\longrightarrow \min _>" width="" height="" />

Аналитическое решение данной задачи: =(X^X)^X^Y>" width="" height="" />
, однако при вырожденности матрицы X>" width="" height="" />
решение оказывается не единственным, а при ее плохой обусловленности — неустойчивым. Поэтому целесообразно ввести регуляризацию по параметру " width="" height="" />
, например, >" width="" height="" />
.

Таким образом, приходим к следующей задаче минимизации (гребневая (ridge) регрессия):

$<\displaystyle Q(\beta )=\left\|Y-X\beta \right\|^ +\lambda \left\|\beta \right\|^\longrightarrow \min _>$

$<\displaystyle \left\|\beta \right\|^ где =\sum _^>^,>$
" width="" height="" />
— параметр регуляризации(неотрицательное число).

Вывод оптимальных весов [ ]

$<\displaystyle \beta > Для нахождения оптимальных весов продифференцируем функционал по$
и приравняем к 0: <\partial \beta >>=2X^(X\beta -Y)+2\lambda \beta =0>" width="" height="" />

$<\displaystyle (X^ X+\lambda I)\beta =X^Y>$

$<\displaystyle \beta ^<*> =(X^X+\lambda I)^X^Y>$
При увеличении параметра " width="" height="" />
решение становится более устойчивым, но с другой стороны — смещенным. При уменьшении — приходим к задаче ОНК без регуляризации: имеем шанс переобучиться. Поэтому нужно искать что-то посерединке.

Обобщение через ядра [ ]

Решение прямой (см. выше) задачи, как уже было получено: =(X^X+\lambda I)^X^Y>" width="" height="" />
. Заметим, что в силу неотрицательной определенности матрицы X>" width="" height="" />
матрица X+\lambda I>" width="" height="" />
вообще положительно определена, поэтому прямое решение всегда существует и единственно. Сложность обучения: (N+D))>" width="" height="" />
, сложность предсказания: " width="" height="" />
.

Введем двойственные переменные. Для этого решим двойственную задачу, где решение прямой задачи будет представлено в виде некоторой линейной комбинации векторов обучающей выборки. Из условий стационарности (X\beta -Y)+\lambda \beta =0>" width="" height="" />
следует <\lambda >>X^(Y-X\beta )=X^\alpha >" width="" height="" />
, где вектор <\lambda >>(Y-X\beta )>" width="" height="" />
— вектор двойственных переменных. Формула для предсказания: >(x)=x^\beta =x^X^\alpha =\sum _^\alpha _\langle x,x_\rangle >" width="" height="" />
. Найти двойственные переменные можно следующим образом: +\lambda I)^Y>" width="" height="" />
. Это прямо следует из <\lambda >>(Y-X\beta )>" width="" height="" />
при подстановке \alpha >" width="" height="" />
. Сложность обучения: (D+N))>" width="" height="" />
, сложность предсказания: " width="" height="" />
.

Заметим, что для нахождения двойственных переменных и предсказания по ним требуются лишь скалярные произведения векторов обучающей выборки, но тогда, используя общую парадигму везде выше на ядерную функцию , получив следующие формулы: Y>" width="" height="" />
, где _=K(x_,x_)>" width="" height="" />
— матрица Грама, >(x)=\sum _^\alpha _K(x,x_)>" width="" height="" />
. Таким образом, решая задачу линейной регрессии можно получать нелинейные решения.

Читайте также: